Hybrid plasmonic leaky-mode lasing on subwavelength scale
doi: 10.37188/CO.2020-0108
-
摘要: 由于光存在衍射极限,因此传统方法不能实现亚波长尺度下的金宝搏188软件怎么用 激射。为了打破这一衍射极限,本文设计了金属-介电层-半导体堆叠结构来实现深亚波长尺度下的金宝搏188软件怎么用 激射,并讨论了相关结构对模式传播的影响。结构设计上,采用低介电常数金属银作为衬底、10 nm厚的LiF作为介电层、具有六边形截面的半导体纳米线ZnO作为高介电常数层,采用有限差分本征模和时域有限差分方法对所设计的结构进行光学仿真模拟。首先,通过改变ZnO纳米线的直径,使用有限本征模方法分析介电层中的光学模式,得到4种模式分布。然后,通过这4种光学模式在不同纳米线直径下的有效折射率和损耗计算了对应的波导传输距离以及激射阈值增益。最后,采用三维时域有限差分方法仿真分析纳米线稳态金宝搏188软件怎么用 发射过程中各模式的电场分布。结果表明:在纳米线和金属衬底之间的介电层上存在混合等离子体模式和混合电模式,对于直径低于75 nm的ZnO纳米线,没有有效的物理光学模式,即混合等离子体模式和混合电模式都被切断,当ZnO纳米线的直径大于75 nm时,混合等离子体模式可以有效存在,而混合电模式在ZnO纳米线的直径达到120 nm之后才出现。虽然混合等离子体模式可以更好地限制在介电层中,但是它们的模式损耗太大,传播距离相对较小。此外,与混合等离子体模式相比,混合电模式的传播距离更长。在给定微米线的直径(D = 240 μm)下,混合电模式传播距离超过50 μm。综上可知,在深亚波长尺度下利用混合泄漏模式可以打破光学衍射极限并实现金宝搏188软件怎么用 激射。
-
关键词:
- 金宝搏188软件怎么用 /
- 泄漏模式 /
- 亚波长 /
- 波导
Abstract: Due to the existence of diffraction limit as the basic characteristic of light, the lasing on subwavelength scale cannot be achieved by traditional methods. In order to break this diffraction limit, a stacked structure composed of metal, dielectric layer and semiconductor was designed in this paper to achieve lasing on the deep subwavelength scale and its influence on the propagation mode was discussed. In terms of structural design, we used silver, a metal with low dielectric constant, as the substrate, a 10 nm-thick LiF layer as the dielectric layer, and a ZnO semiconductor nanowire with hexagonal section as the high-dielectric-constant layer. We adopted the finite-difference eigen mode and Finite-Difference Time-Domain (FDTD) method to perform optical simulation of the designed structure. First, by changing the nanowire diameter and using the finite eigen mode, the optical modes in the dielectric layer were analyzed to obtain four mode distributions. Then the effective refractive indexes and losses of the four optical modes at different nanowire diameters were used to calculate the corresponding waveguide propagation distances and lasing threshold gains. Finally, the three-dimensional FDTD method was introduced to simulate the electric field distribution of the four modes during the steady-state laser emissionin of the nanowire. The results showed that there were hybrid plasmonic mode and hybrid electric mode in the dielectric layer between the nanowire and the metal substrate. When the diameter of ZnO nanowire was smaller than 75 nm, there was no effective physical optical mode, that is, both the hybrid plasmonic mode and the hybrid electric mode were cut off. When the nanowire diameter was larger than 75 nm, the hybrid plasmonic mode could effectively exist. The hybrid electric mode did not appear until the nanowire diameter reached 120 nm. Although the hybrid plasmonic mode could be better confined to the dielectric layer, its loss was too large and its propagation distance was relatively small. In addition, the hybrid electric mode traveled a longer distance than hybrid plasmonic mode. At the given diameter of the micron wire (D = 240 μm), the hybrid electric mode propagated for over 50 μm. In conclusion, the hybrid leaky mode on the deep subwavelength scale can break the optical diffraction limit and realize lasing.-
Key words:
- laser /
- leaky-mode /
- subwavelength /
- waveguide
-
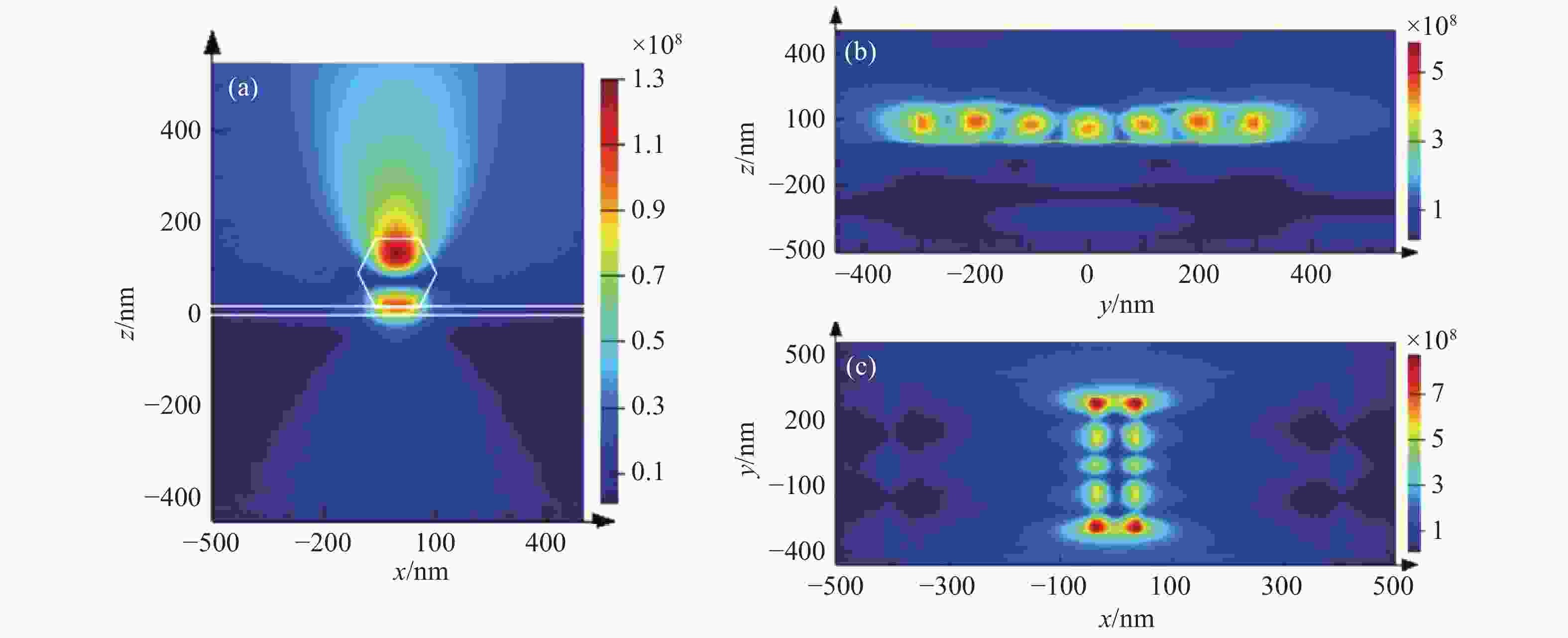
Figure 7. Snapshots of the HE1 lasing mode electric field intensity distribution in three different section directions. (a) xz plane and (b) yz plane of the cross section of the nanowire-dielectric-metal interface; (c) xy plane inside the dielectric layer (z = 0). The diameter of the ZnO nanowire in the above simulation was set to be 170 nm.
-
[1] RUST M J, BATES M, ZHUANG X W. Sub-diffraction-limit imaging by stochastic optical reconstruction microscopy (STORM)[J]. Nature Methods, 2006, 3(10): 793-796. doi: 10.1038/nmeth929 [2] MAIER S A, KIK P G, ATWATER H A, et al. Local detection of electromagnetic energy transport below the diffraction limit in metal nanoparticle plasmon waveguides[J]. Nature Materials, 2003, 2(4): 229-232. doi: 10.1038/nmat852 [3] GRAMOTNEV D K, BOZHEVOLNYI S I. Plasmonics beyond the diffraction limit[J]. Nature Photonics, 2010, 4(2): 83-91. doi: 10.1038/nphoton.2009.282 [4] BARNES W L, DEREUX A, EBBESEN T W. Surface plasmon subwavelength optics[J]. Nature, 2003, 424(6950): 824-830. doi: 10.1038/nature01937 [5] BOZHEVOLNYI S I, VOLKOV V S, DEVAUX E, et al. Channel plasmon subwavelength waveguide components including interferometers and ring resonators[J]. Nature, 2006, 440(7083): 508-511. doi: 10.1038/nature04594 [6] PARK S, HAHN J W. Plasmonic data storage medium with metallic nano-aperture array embedded in dielectric material[J]. Optics Express, 2009, 17(22): 20203-20210. doi: 10.1364/OE.17.020203 [7] MANSURIPUR M, ZAKHARIAN A R, LESUFFLEUR A, et al. Plasmonic nano-structures for optical data storage[J]. Optics Express, 2009, 17(16): 14001-14014. doi: 10.1364/OE.17.014001 [8] KUBO A, PONTIUS N, PETEK H. Femtosecond microscopy of surface plasmon polariton wave packet evolution at the silver/vacuum interface[J]. Nano Letters, 2007, 7(2): 470-475. doi: 10.1021/nl0627846 [9] SMOLYANINOV I I, ELLIOTT J, ZAYATS A V, et al. Far-field optical microscopy with a nanometer-scale resolution based on the in-plane image magnification by surface plasmon polaritons[J]. Physical Review Letters, 2005, 94(5): 057401. doi: 10.1103/PhysRevLett.94.057401 [10] NELSON B P, GRIMSRUD T E, LILES M R, et al. Surface plasmon resonance imaging measurements of DNA and RNA hybridization adsorption onto DNA microarrays[J]. Analytical Chemistry, 2001, 73(1): 1-7. doi: 10.1021/ac0010431 [11] SMITH E A, THOMAS W D, KIESSLING L L, et al. Surface plasmon resonance imaging studies of protein-carbohydrate interactions[J]. Journal of the American Chemical Society, 2003, 125(20): 6140-6148. doi: 10.1021/ja034165u [12] LEE Y H, JEWELL J L, SCHERER A, et al. Room-temperature continuous-wave vertical-cavity single-quantum-well microlaser diodes[J]. Electronics Letters, 1989, 25(20): 1377-1378. doi: 10.1049/el:19890921 [13] LEVI A F J, SLUSHER R E, MCCALL S L, et al. Room temperature operation of microdisc lasers with submilliamp threshold current[J]. Electronics Letters, 1992, 28(11): 1010-1012. doi: 10.1049/el:19920642 [14] PAINTER O, LEE R K, SCHERER A, et al. Two-dimensional photonic band-gap defect mode laser[J]. Science, 1999, 284(5421): 1819-1821. doi: 10.1126/science.284.5421.1819 [15] MA R M, OULTON R F, SORGER V J, et al. Room-temperature sub-diffraction-limited plasmon laser by total internal reflection[J]. Nature Materials, 2011, 10(2): 110-113. doi: 10.1038/nmat2919 [16] TREDICUCCI A, GMACHL C, CAPASSO F, et al. Single-mode surface-plasmon laser[J]. Applied Physics Letters, 2000, 76(16): 2164-2166. doi: 10.1063/1.126183 [17] CHU SH, WANG G P, ZHOU W, et al. Electrically pumped waveguide lasing from ZnO nanowires[J]. Nature Nanotechnology, 2011, 6(8): 506-510. doi: 10.1038/nnano.2011.97 [18] JOHNSON J C, CHOI H J, KNUTSEN K P, et al. Single gallium nitride nanowire lasers[J]. Nature Materials, 2002, 1(2): 106-110. doi: 10.1038/nmat728 [19] WUESTNER S, HAMM J M, PUSCH A, et al. Plasmonic leaky-mode lasing in active semiconductor nanowires[J]. Laser &Photonics Reviews, 2015, 9(2): 256-262. [20] NEZHAD M P, SIMIC A, BONDARENKO O, et al. Room-temperature subwavelength metallo-dielectric lasers[J]. Nature Photonics, 2010, 4(6): 395-399. doi: 10.1038/nphoton.2010.88 [21] OULTON R F, SORGER V J, ZENTGRAF T, et al. Plasmon lasers at deep subwavelength scale[J]. Nature, 2009, 461(7264): 629-632. doi: 10.1038/nature08364 [22] OULTON R F, BARTAL G, PILE D F P, et al. Confinement and propagation characteristics of subwavelength plasmonic modes[J]. New Journal of Physics, 2008, 10(10): 105018. doi: 10.1088/1367-2630/10/10/105018 [23] JOHNSON P B, CHRISTY R W. Optical constants of the noble metals[J]. Physical Review B, 1972, 6(12): 4370. doi: 10.1103/PhysRevB.6.4370 [24] NING C Z. Semiconductor nanolasers[J]. Physica Status Solidi (B) :Basic Solid State Physics, 2010, 247(4): 774-788. doi: 10.1002/pssb.200945436 [25] LI D B, NING C ZH. Peculiar features of confinement factors in a metal-semiconductor waveguide[J]. Applied Physics Letters, 2010, 96(18): 181109. doi: 10.1063/1.3425896 [26] LI D B, NING C ZH. Giant modal gain, amplified surface plasmon-polariton propagation, and slowing down of energy velocity in a metal-semiconductor-metal structure[J]. Physical Review B, 2009, 80(15): 153304. doi: 10.1103/PhysRevB.80.153304 [27] CHANG S H, TAFLOVE A. Finite-difference time-domain model of lasing action in a four-level two-electron atomic system[J]. Optics Express, 2004, 12(16): 3827-3833. doi: 10.1364/OPEX.12.003827 [28] ZHU ZH M, BROWN T G. Full-vectorial finite-difference analysis of microstructured optical fibers[J]. Optics Express, 2002, 10(17): 853-864. doi: 10.1364/OE.10.000853 [29] OULTON R F, SORGER V J, GENOV D A, et al. A hybrid plasmonic waveguide for subwavelength confinement and long-range propagation[J]. Nature Photonics, 2008, 2(8): 496-500. doi: 10.1038/nphoton.2008.131 -





 下载:
下载: