-
摘要: 以超表面为代表的二维人工超材料通过其亚波长单元增强光与物质的相互作用,进而操控光的振幅、相位、偏振、轨道角动量等物理量。目前,非平凡拓扑性质的二维人工超材料由于具有鲁棒的光单向传输等性质成为了光学领域的研究重点。拓扑相不仅成为了凝聚态物理领域一种描述物质的新的自由度,也成为描述人工超材料光学性质的一个新的参量。本文从拓扑光子学的起源出发,介绍了二维人工超材料的拓扑性质分类以及最新的拓扑光子学研究进展,并进行了总结与展望。Abstract: Two dimensional artificial metamaterials, represented by metasurfaces, could control the amplitude, phase, polarization and orbital angular momentum of light, through tailoring the interaction between light and matter. Nowadays, two dimensional artificial metamaterials with nontrivial topological properties have become research focus in optics due to their advantages in robust unidirectional transmission. The topological phase is not only a new degree of freedom to describe matter in the field of condensed matter physics, but also a new parameter to describe optical properties of artificial metamaterials. In this review, the origin of topological photonics and classification for topological properties of two dimensional metamaterials are introduced. The latest progress in topological photonics has also been presented. The summary and prospect of topological metamaterials are given at the end of the review.
-
Key words:
- artificial metamaterial /
- topological photonic /
- synthetic dimension
-
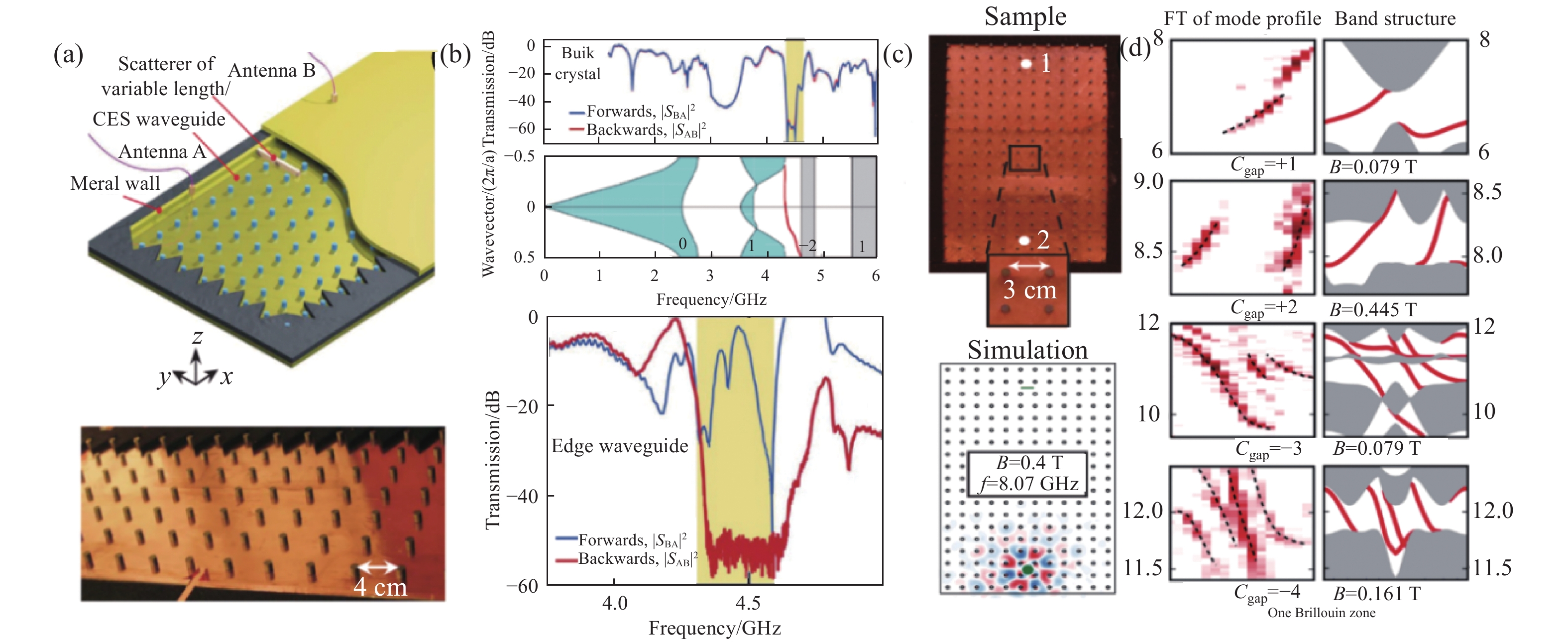
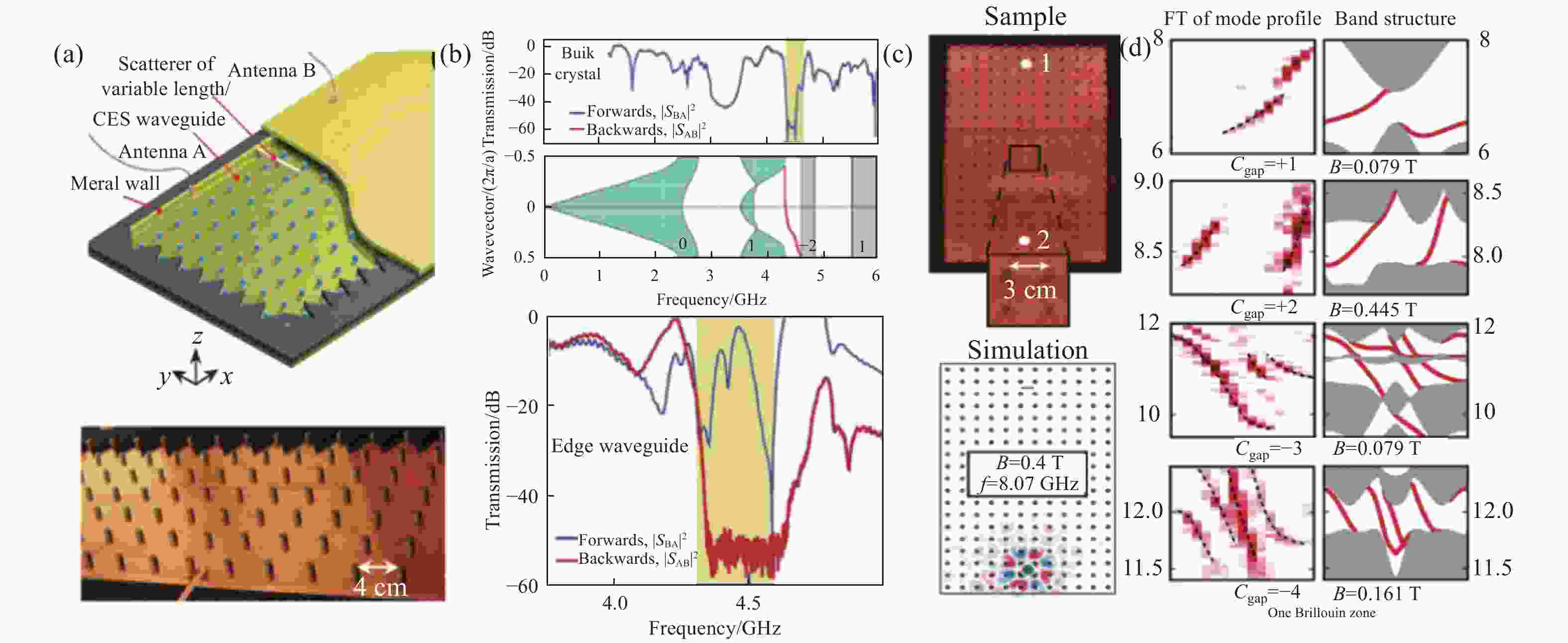
图 1 (a) 利用旋磁材料制备的光学拓扑超材料示意图;(b)实验测试得到的体透射系数,光学拓扑超材料的能带图(标签为能带的陈数)[21],实验测得的边界透射系数;(c)大陈数拓扑光子晶体的实验样品以及仿真结构;(d)实验和计算得到的能带结构[24]
Figure 1. (a) Structure diagram of optical topological metastructure fabricated by gyromagnetic material; (b) experimental bulk transmission and band structure of optical topological metastructure[21]; (c) topological photonics crystal sample and simulation scheme with large chern number; (d) band structure obtained by experiment and calculation[24]
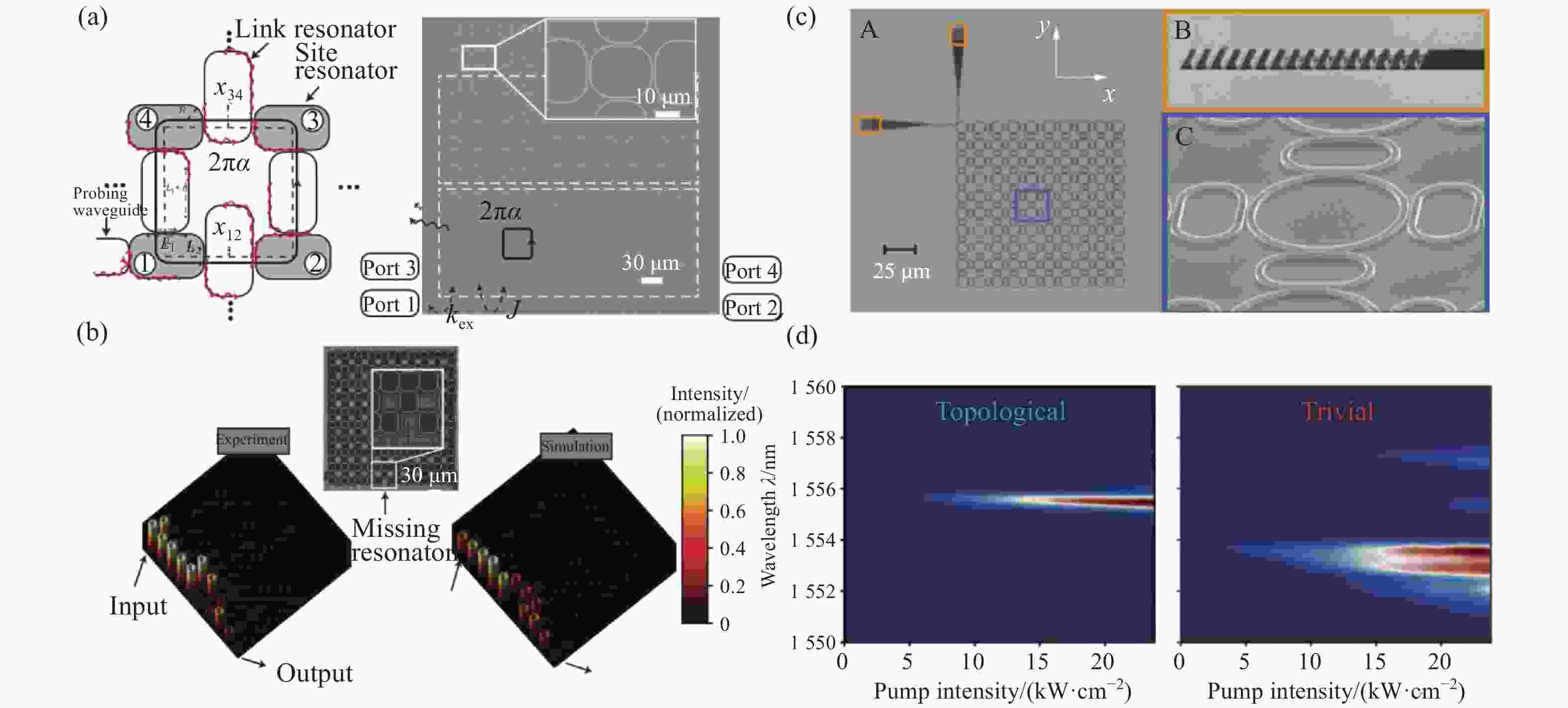
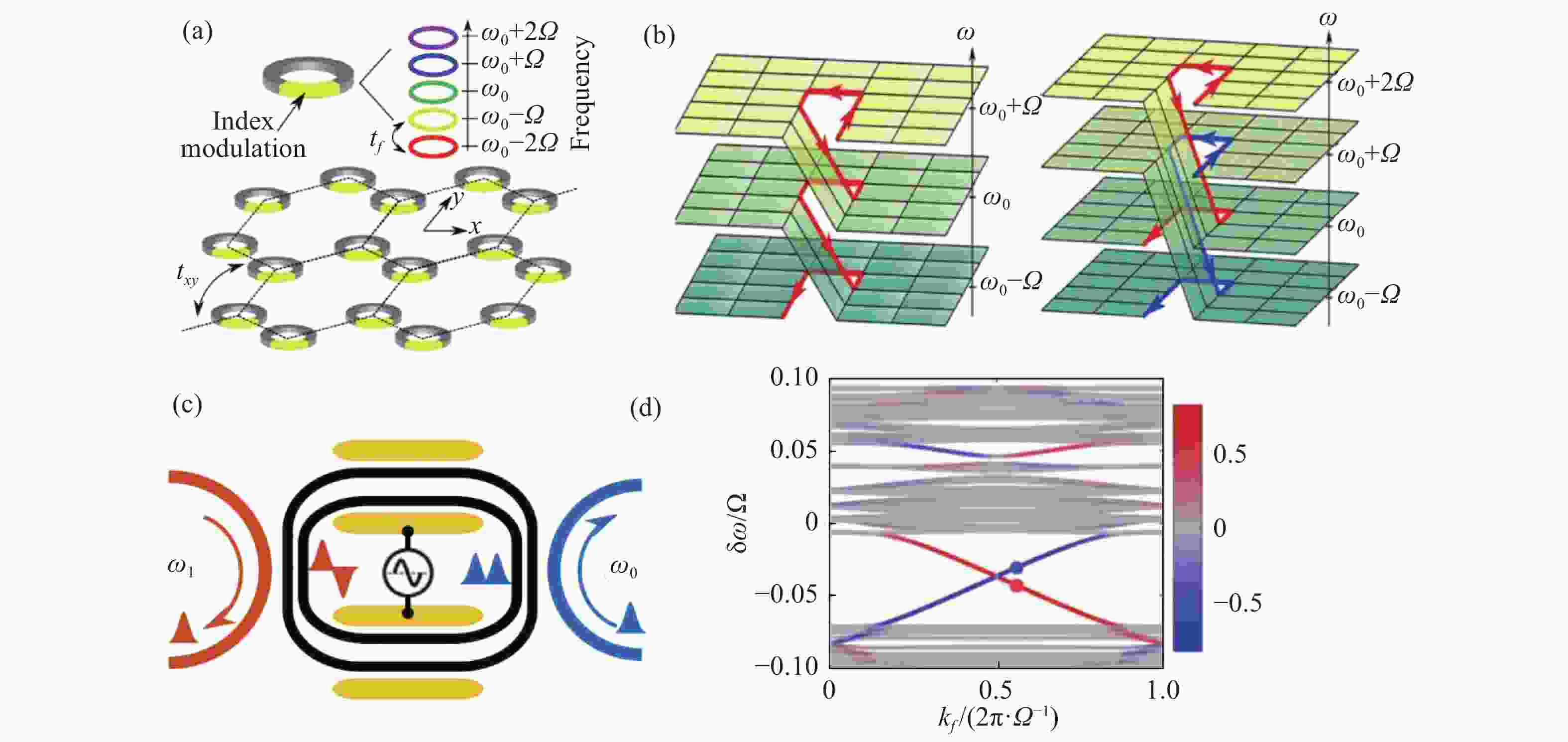
图 2 (a)单个单元的耦合环形波导示意图以及实验测试系统;(b)实验测试得到免疫缺陷的鲁棒的边界传输[28];(c)拓扑金宝搏188软件怎么用 器结构SEM图;(d)拓扑金宝搏188软件怎么用 器和拓扑平凡金宝搏188软件怎么用 器在不同泵浦强度下的激发光谱[31]
Figure 2. (a) Scheme diagram and experimental setup for each ring coupling unit; (b) defect-imunne robust edge transmission by experimental mearsurement[28]; (c) SEM images of topological laser; (d) emission spectra of topological and trivial laser under different bump intensity[31]
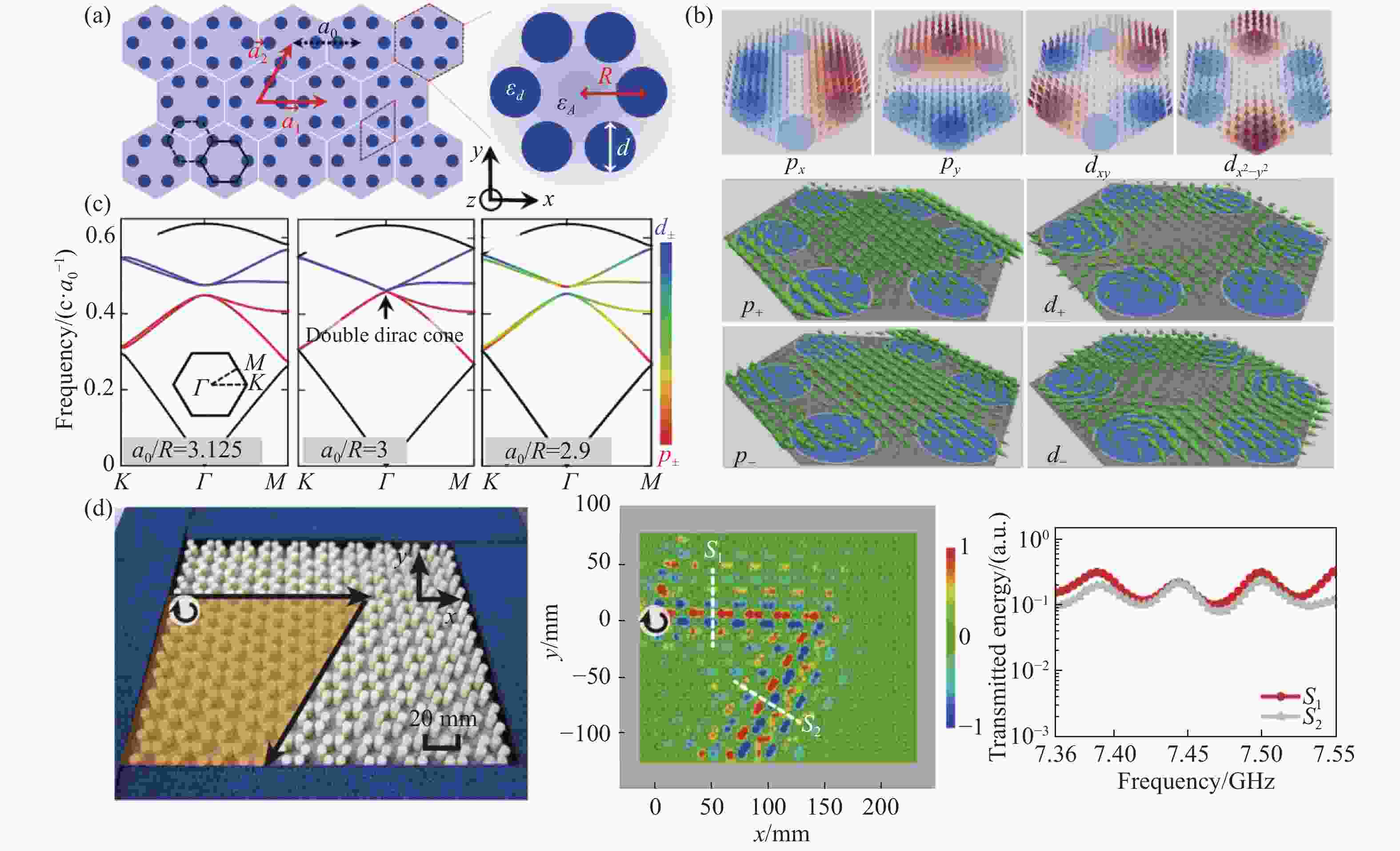
图 3 (a)拓扑光子晶体示意图[32];(b)
$ {p}_{x}\left({p}_{y}\right) $ 和$ {d}_{xy}\left({d}_{{x}^{2}-{y}^{2}}\right) $ 构成的赝自旋态[32];(c)光学拓扑结构能带图[32];(d)Al2O3柱构成的光学拓扑结构、实验测试得到的7.41 GHz频率时场分布、在S1点和S2点的透射强度[34]Figure 3. (a) Schemetic diagram of topological photonic crystal[32]; (b) pseudo-spin states of
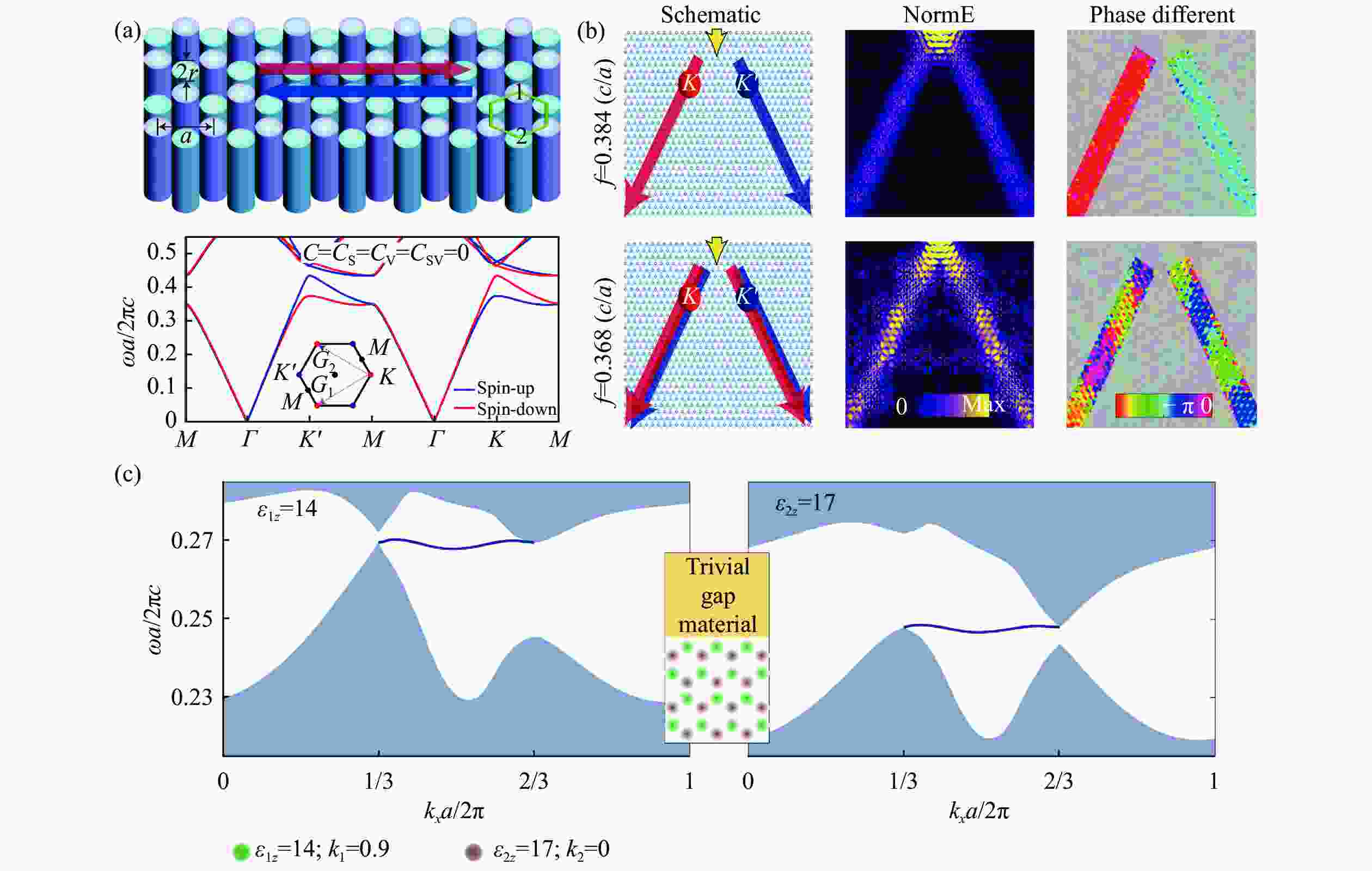
$ {p}_{x}\left({p}_{y}\right) $ and$ {d}_{xy}\left({d}_{{x}^{2}-{y}^{2}}\right) $ [32]; (c) band structure of topological optical structure[32]; (d) topological optical structure consisiting of Al2O3 pillars, field distribution with frequency of 7.41 GHz in experimental, transmitted energy at S1 and S2[34]图 4 (a)利用能谷自由度设计的光学拓扑结构[43];(b)能谷依赖的光学拓扑结构的自旋分离行为[43];(c)左右分别为介电常数为14和17时自旋向上的体态投影以及受拓扑保护的平边界态[43]
Figure 4. (a)Optical topological structure designed by energy valley freedom[43]; (b) spin separation behavior in valley dependent optical topological structure[43]; (c) flat edge dispersions in a photonic crystal with different permittivtities. Only the spin-up polarized projection bands (shaded blue region) and the spin-up edge states are illustrated [43]
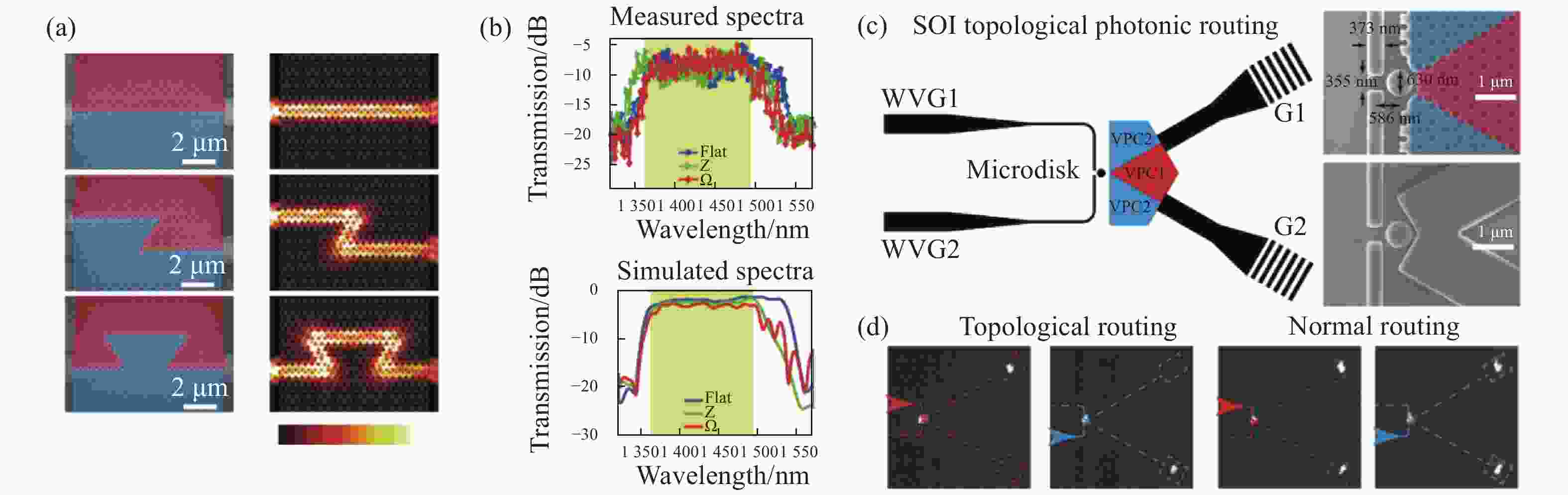
图 5 (a)利用硅基板设计的具有不同边界的能谷依赖光学拓扑结构[44];(b)实验和仿真得到的对不同边界路径的透射[44];(c)光子路由示意图[44];(d)光子路由的拓扑光传输[44]
Figure 5. (a) Topological optical structure on the substrate of Si with different boundary[44]; (b) transmission spectra obtained by experiment and simulation[44]; (c) schemetic diagram of photon route[44]; (d) topological optical transimission of photon route[44]
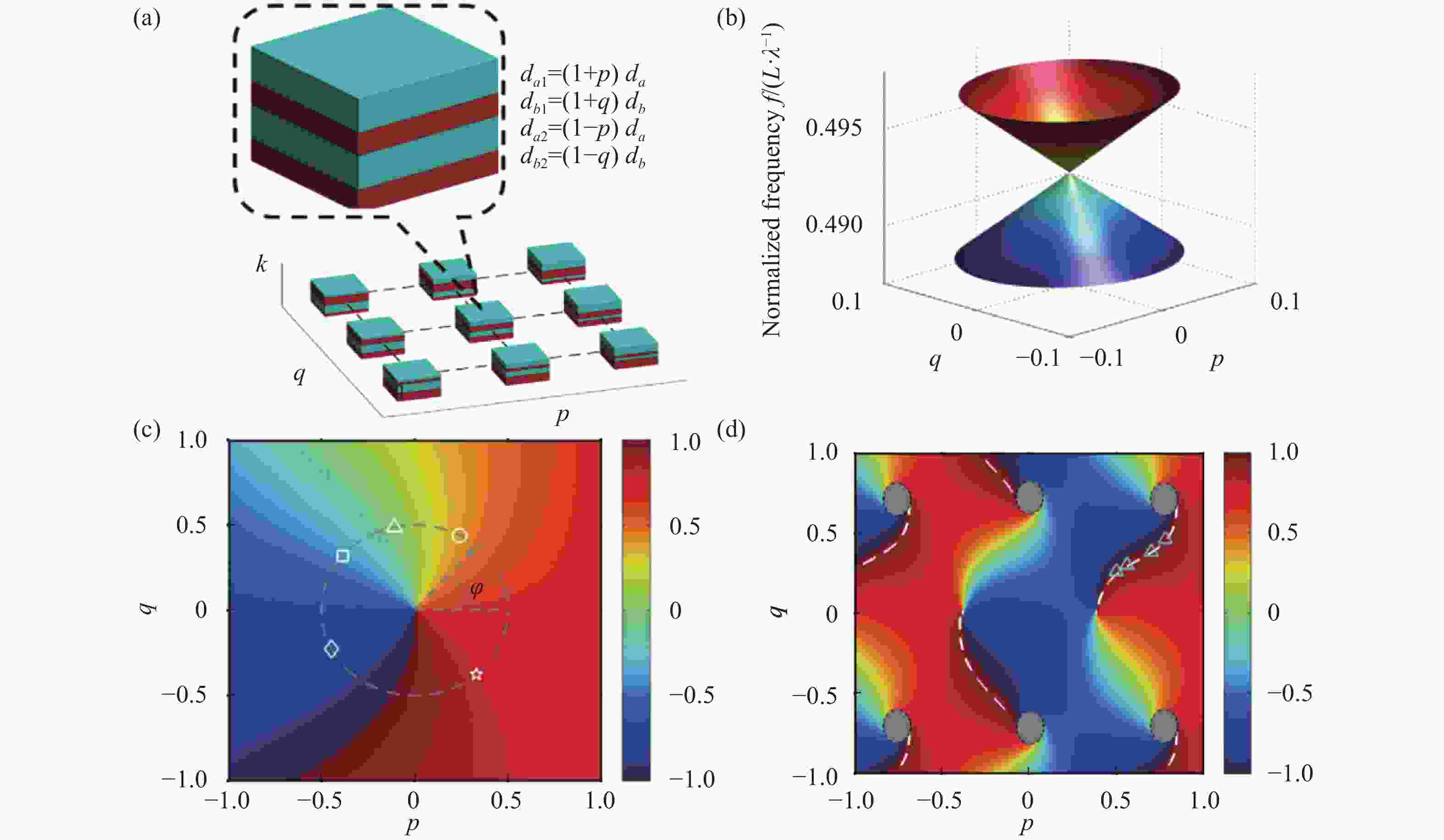
图 6 (a)利用介质层厚度构建参数空间示意图[66];(b)在三维合成维度中的人工外尔点[66];(c)光子晶体截断面上的反射相位分布[66];(d)在外尔点频率处的反射相位,白色虚线为费米弧轨迹[66]
Figure 6. (a) Schematic diagram of parameter space constructed by dielectric thickness[66]; (b) artificial Weyl point in 3 synthetic dimensional topological structure[66]; (c) reflection phase on the truncated face of photonic crystal[66]; (d) reflection phase at Weyl point, Fermi arc is marked in white dashed line[66]
-
[1] LIU Y M, ZHANG X. Metamaterials: a new frontier of science and technology[J]. Chemical Society Reviews, 2011, 40(5): 2494-2507. doi: 10.1039/c0cs00184h [2] MINOVICH A E, MIROSHNICHENKO A E, BYKOV A Y, et al. Functional and nonlinear optical metasurfaces[J]. Laser &Photonics Reviews, 2015, 9(2): 195-213. [3] YU N F, CAPASSO F. Flat optics with designer metasurfaces[J]. Nature Materials, 2014, 13: 139. doi: 10.1038/nmat3839 [4] ZHENG G X, MÜHLENBERND H, KENNEY M, et al. Metasurface holograms reaching 80% efficiency[J]. Nature Nanotechnology, 2015, 10(4): 308-312. doi: 10.1038/nnano.2015.2 [5] LEE J, TYMCHENKO M, ARGYROPOULOS C, et al. Giant nonlinear response from plasmonic metasurfaces coupled to intersubband transitions[J]. Nature, 2014, 511(7507): 65-69. doi: 10.1038/nature13455 [6] KILDISHEV A V, BOLTASSEVA A, SHALAEV V M. Planar photonics with metasurfaces[J]. Science, 2013, 339(6125): 1232009. doi: 10.1126/science.1232009 [7] LIN D M, FAN P Y, HASMAN E, et al. Dielectric gradient metasurface optical elements[J]. Science, 2014, 345(6194): 298-302. doi: 10.1126/science.1253213 [8] LU L, JOANNOPOULOS J D, SOLJAČIĆ M. Topological photonics[J]. Nature Photonics, 2014, 8(11): 821-829. doi: 10.1038/nphoton.2014.248 [9] OZAWA T, PRICE H M, AMO A, et al. Topological photonics[J]. Reviews of Modern Physics, 2019, 91(1): 015006. doi: 10.1103/RevModPhys.91.015006 [10] THOULESS D J, KOHMOTO M, NIGHTINGALE M P, et al. Quantized hall conductance in a two-dimensional periodic potential[J]. Physical Review Letters, 1982, 49(6): 405-408. doi: 10.1103/PhysRevLett.49.405 [11] KANE C L, MELE E J. Z 2 topological order and the quantum spin Hall effect[J]. Physical Review Letters, 2005, 95(14): 146802. doi: 10.1103/PhysRevLett.95.146802 [12] KANE C L, MELE E J. Quantum spin Hall effect in graphene[J]. Physical Review Letters, 2005, 95(22): 226801. doi: 10.1103/PhysRevLett.95.226801 [13] BERNEVIG B A, HUGHES T L, ZHANG SH CH. Quantum spin Hall effect and topological phase transition in HgTe quantum wells[J]. Science, 2006, 314(5806): 1757-1761. doi: 10.1126/science.1133734 [14] BERNEVIG B A, ZHANG SH CH. Quantum spin Hall effect[J]. Physical Review Letters, 2006, 96(10): 106802. doi: 10.1103/PhysRevLett.96.106802 [15] HASAN M Z, KANE C L. Colloquium: topological insulators[J]. Reviews of Modern Physics, 2010, 82(4): 3045-3067. doi: 10.1103/RevModPhys.82.3045 [16] QI X L, ZHANG SH CH. Topological insulators and superconductors[J]. Reviews of Modern Physics, 2011, 83(4): 1057-1110. doi: 10.1103/RevModPhys.83.1057 [17] HALDANE F D M, RAGHU S. Possible realization of directional optical waveguides in photonic crystals with broken time-reversal symmetry[J]. Physical Review Letters, 2008, 100(1): 013904. doi: 10.1103/PhysRevLett.100.013904 [18] HATSUGAI Y. Chern number and edge states in the integer quantum Hall effect[J]. Physical Review Letters, 1993, 71(22): 3697-3700. doi: 10.1103/PhysRevLett.71.3697 [19] FUKUI T, HATSUGAI Y, SUZUKI H. Chern numbers in discretized brillouin zone: efficient method of computing (Spin) hall conductances[J]. Journal of the Physical Society of Japan, 2005, 74(6): 1674-1677. doi: 10.1143/JPSJ.74.1674 [20] RAGHU S, HALDANE F D M. Analogs of quantum-Hall-effect edge states in photonic crystals[J]. Physical Review A, 2008, 78(3): 033834. doi: 10.1103/PhysRevA.78.033834 [21] WANG ZH, CHONG Y D, JOANNOPOULOS J D, et al. Observation of unidirectional backscattering-immune topological electromagnetic states[J]. Nature, 2009, 461(7265): 772-775. doi: 10.1038/nature08293 [22] WANG ZH, CHONG Y D, JOANNOPOULOS J D, et al. Reflection-free one-way edge modes in a gyromagnetic photonic crystal[J]. Physical Review Letters, 2008, 100(1): 013905. doi: 10.1103/PhysRevLett.100.013905 [23] SKIRLO S A, LU L, SOLJAČIĆ M. Multimode one-way waveguides of large chern numbers[J]. Physical Review Letters, 2014, 113(11): 113904. doi: 10.1103/PhysRevLett.113.113904 [24] SKIRLO S A, LU L, IGARASHI Y, et al. Experimental observation of large chern numbers in photonic crystals[J]. Physical Review Letters, 2015, 115(25): 253901. doi: 10.1103/PhysRevLett.115.253901 [25] FANG CH, LU L, LIU J W, et al. Topological semimetals with helicoid surface states[J]. Nature Physics, 2016, 12(10): 936-941. doi: 10.1038/nphys3782 [26] FU L, KANE C L. Topological insulators with inversion symmetry[J]. Physical Review B, 2007, 76(4): 045302. doi: 10.1103/PhysRevB.76.045302 [27] YU R, QI X L, BERNEVIG A, et al. Equivalent expression of Z 2 topological invariant for band insulators using the non-Abelian Berry connection[J]. Physical Review B, 2011, 84(7): 075119. doi: 10.1103/PhysRevB.84.075119 [28] HAFEZI M, MITTAL S, FAN J, et al. Imaging topological edge states in silicon photonics[J]. Nature Photonics, 2013, 7(12): 1001-1005. doi: 10.1038/nphoton.2013.274 [29] HAFEZI M, DEMLER E A, LUKIN M D, et al. Robust optical delay lines with topological protection[J]. Nature Physics, 2011, 7(11): 907-912. doi: 10.1038/nphys2063 [30] HARARI G, BANDRES M A, LUMER Y, et al. Topological insulator laser: theory[J]. Science, 2018, 359(6381): eaar4003. doi: 10.1126/science.aar4003 [31] BANDRES M A, WITTEK S, HARARI G, et al. Topological insulator laser: experiments[J]. Science, 2018, 359(6381): eaar4005. doi: 10.1126/science.aar4005 [32] WU L H, HU X. Scheme for achieving a topological photonic crystal by using dielectric material[J]. Physical Review Letters, 2015, 114(22): 223901. doi: 10.1103/PhysRevLett.114.223901 [33] WU L H, HU X. Topological properties of electrons in honeycomb lattice with detuned hopping energy[J]. Scientific Reports, 2016, 6: 24347. doi: 10.1038/srep24347 [34] YANG Y T, XU Y F, XU T, et al. Visualization of a unidirectional electromagnetic waveguide using topological photonic crystals made of dielectric materials[J]. Physical Review Letters, 2018, 120(21): 217401. doi: 10.1103/PhysRevLett.120.217401 [35] ZHANG ZH W, WEI Q, CHENG Y, et al. Topological creation of acoustic pseudospin multipoles in a flow-free symmetry-broken metamaterial lattice[J]. Physical Review Letters, 2017, 118(8): 084303. doi: 10.1103/PhysRevLett.118.084303 [36] GORLACH M A, NI X, SMIRNOVA D A, et al. Far-field probing of leaky topological states in all-dielectric metasurfaces[J]. Nature Communications, 2018, 9(1): 909. doi: 10.1038/s41467-018-03330-9 [37] SHAO Z K, CHEN H ZH, WANG S, et al. A high-performance topological bulk laser based on band-inversion-induced reflection[J]. Nature Nanotechnology, 2020, 15(1): 67-72. doi: 10.1038/s41565-019-0584-x [38] SMIRNOVA D, KRUK S, LEYKAM D, et al. Third-harmonic generation in photonic topological metasurfaces[J]. Physical Review Letters, 2019, 123(10): 103901. doi: 10.1103/PhysRevLett.123.103901 [39] PROCTOR M, CRASTER R V, MAIER S A, et al. Exciting pseudospin-dependent edge states in plasmonic metasurfaces[J]. ACS Photonics, 2019, 6(11): 2985-2995. doi: 10.1021/acsphotonics.9b01192 [40] LEE J, MAK K F, SHAN J. Electrical control of the valley Hall effect in bilayer MoS2 transistors[J]. Nature Nanotechnology, 2016, 11(5): 421-425. doi: 10.1038/nnano.2015.337 [41] MAK K F, MCGILL K L, PARK J, et al. Valleytronics. The valley Hall effect in MoS2 transistors[J]. Science, 2014, 344(6191): 1489-1492. doi: 10.1126/science.1250140 [42] SCHAIBLEY J R, YU H Y, CLARK G, et al. Valleytronics in 2D materials[J]. Nature Reviews Materials, 2016, 1(11): 16055. doi: 10.1038/natrevmats.2016.55 [43] DONG J W, CHEN X D, ZHU H Y, et al. Valley photonic crystals for control of spin and topology[J]. Nature Materials, 2017, 16(3): 298-302. doi: 10.1038/nmat4807 [44] HE X T, LIANG E T, YUAN J J, et al. A silicon-on-insulator slab for topological valley transport[J]. Nature Communications, 2019, 10(1): 872. doi: 10.1038/s41467-019-08881-z [45] YANG Y H, YAMAGAMI Y, YU X B, et al. Terahertz topological photonics for on-chip communication[J]. Nature Photonics, 2020, 14(7): 446-451. doi: 10.1038/s41566-020-0618-9 [46] GONG Y K, WONG S, BENNETT A J, et al. Topological insulator laser using valley-hall photonic crystals[J]. ACS Photonics, 2020, 7(8): 2089-2097. doi: 10.1021/acsphotonics.0c00521 [47] WU X X, MENG Y, TIAN J X, et al. Direct observation of valley-polarized topological edge states in designer surface plasmon crystals[J]. Nature Communications, 2017, 8(1): 1304. doi: 10.1038/s41467-017-01515-2 [48] KANG Y H, NI X, CHENG X J, et al. Pseudo-spin-valley coupled edge states in a photonic topological insulator[J]. Nature Communications, 2018, 9(1): 3029. doi: 10.1038/s41467-018-05408-w [49] GAO F, XUE H R, YANG ZH J, et al. Topologically protected refraction of robust kink states in valley photonic crystals[J]. Nature Physics, 2018, 14(2): 140-144. doi: 10.1038/nphys4304 [50] MA T, SHVETS G. All-Si valley-Hall photonic topological insulator[J]. New Journal of Physics, 2016, 18(2): 025012. doi: 10.1088/1367-2630/18/2/025012 [51] NOH J, HUANG SH, CHEN K P, et al. Observation of photonic topological valley hall edge states[J]. Physical Review Letters, 2018, 120(6): 063902. doi: 10.1103/PhysRevLett.120.063902 [52] GAO ZH, YANG ZH J, GAO F, et al. Valley surface-wave photonic crystal and its bulk/edge transport[J]. Physical Review B, 2017, 96(20): 201402. doi: 10.1103/PhysRevB.96.201402 [53] NI X, PURTSELADZE D, SMIRNOVA D A, et al. Spin- and valley-polarized one-way Klein tunneling in photonic topological insulators[J]. Science Advances, 2018, 4(5): eaap8802. doi: 10.1126/sciadv.aap8802 [54] CHEN W J, XIAO M, CHAN C T. Photonic crystals possessing multiple Weyl points and the experimental observation of robust surface states[J]. Nature Communications, 2016, 7: 13038. doi: 10.1038/ncomms13038 [55] LU L, FU L, JOANNOPOULOS J D, et al. Weyl points and line nodes in gyroid photonic crystals[J]. Nature Photonics, 2013, 7(4): 294-299. doi: 10.1038/nphoton.2013.42 [56] LI F, HUANG X Q, LU J Y, et al. Weyl points and Fermi arcs in a chiral phononic crystal[J]. Nature Physics, 2017, 14(1): 30-34. [57] YANG Z J, ZHANG B L. Acoustic type-II weyl nodes from stacking dimerized chains[J]. Physical Review Letters, 2016, 117(22): 224301. doi: 10.1103/PhysRevLett.117.224301 [58] LU L, WANG ZH Y, YE D X, et al. Experimental observation of Weyl points[J]. Science, 2015, 349(6248): 622-624. doi: 10.1126/science.aaa9273 [59] YANG B, GUO Q H, TREMAIN B, et al. Ideal Weyl points and helicoid surface states in artificial photonic crystal structures[J]. Science, 2018, 359(6379): 1013-1016. doi: 10.1126/science.aaq1221 [60] YUAN L Q, LIN Q, XIAO M, et al. Synthetic dimension in photonics[J]. Optica, 2018, 5(11): 1369-1405. [61] JIAN CH M, XU C K. Interacting topological insulators with synthetic dimensions[J]. Physical Review X, 2018, 8(4): 041030. doi: 10.1103/PhysRevX.8.041030 [62] LI Q C, JIANG X Y. Singularity induced topological transition of different dimensions in one synthetic photonic system[J]. Optics Communications, 2019, 440: 32-40. doi: 10.1016/j.optcom.2019.02.015 [63] YUAN L Q, XIAO M, LIN Q, et al. Synthetic space with arbitrary dimensions in a few rings undergoing dynamic modulation[J]. Physical Review B, 2018, 97(10): 104105. doi: 10.1103/PhysRevB.97.104105 [64] CHALOPIN T, SATOOR T, EVRARD A, et al. Probing chiral edge dynamics and bulk topology of a synthetic Hall system[J]. Nature Physics, 2020, 16(10): 1017-1021. doi: 10.1038/s41567-020-0942-5 [65] LUO X W, ZHANG J, ZHANG CH W. Tunable flux through a synthetic Hall tube of neutral fermions[J]. Physical Review A, 2020, 102(6): 063327. doi: 10.1103/PhysRevA.102.063327 [66] WANG Q, XIAO M, LIU H, et al. Optical interface states protected by synthetic Weyl points[J]. Physical Review X, 2017, 7(3): 031032. doi: 10.1103/PhysRevX.7.031032 [67] LIN Q, XIAO M, YUAN L Q, et al. Photonic Weyl point in a two-dimensional resonator lattice with a synthetic frequency dimension[J]. Nature Communications, 2016, 7: 13731. doi: 10.1038/ncomms13731 [68] YUAN L Q, SHI Y, FAN SH H. Photonic gauge potential in a system with a synthetic frequency dimension[J]. Optics Letters, 2016, 41(4): 741-744. doi: 10.1364/OL.41.000741 [69] LIN Q, SUN X Q, XIAO M, et al. A three-dimensional photonic topological insulator using a two-dimensional ring resonator lattice with a synthetic frequency dimension[J]. Science Advances, 2018, 4(10): eaat2774. doi: 10.1126/sciadv.aat2774 [70] OZAWA T, PRICE H M, GOLDMAN N, et al. Synthetic dimensions in integrated photonics: from optical isolation to four-dimensional quantum Hall physics[J]. Physical Review A, 2016, 93(4): 043827. doi: 10.1103/PhysRevA.93.043827 [71] MINKOV M, SAVONA V. Haldane quantum Hall effect for light in a dynamically modulated array of resonators[J]. Optica, 2016, 3(2): 200-206. doi: 10.1364/OPTICA.3.000200 [72] MIDYA B, ZHAO H, FENG L. Non-Hermitian photonics promises exceptional topology of light[J]. Nature Communications, 2018, 9(1): 2674. doi: 10.1038/s41467-018-05175-8 [73] ZHANG L, YANG Y H, LIN ZH K, et al. Higher-order topological states in surface-wave photonic crystals[J]. Advanced Science, 2020, 7(6): 1902724. doi: 10.1002/advs.201902724 [74] BENALCAZAR W A, BERNEVIG B A, HUGHES T L. Quantized electric multipole insulators[J]. Science, 2017, 357(6346): 61-66. doi: 10.1126/science.aah6442 [75] SERRA-GARCIA M, PERI V, SÜSSTRUNK R, et al. Observation of a phononic quadrupole topological insulator[J]. Nature, 2018, 555(7696): 342-345. doi: 10.1038/nature25156 [76] ZHANG W X, XIE X, HAO H M, et al. Low-threshold topological nanolasers based on the second-order corner state[J]. Light:Science &Applications, 2020, 9: 109. [77] XIE B Y, SU G X, WANG H F, et al. Higher-order quantum spin Hall effect in a photonic crystal[J]. Nature Communications, 2020, 11(1): 3768. doi: 10.1038/s41467-020-17593-8 [78] XIE B Y, WANG H F, WANG H X, et al. Second-order photonic topological insulator with corner states[J]. Physical Review B, 2018, 98(20): 205147. doi: 10.1103/PhysRevB.98.205147 -





 下载:
下载: