逐像素调制的高反光表面三维测量方法 -

姓名
邮箱
手机号码
标题
留言内容
验证码

逐像素调制的高反光表面三维测量方法

doi:10.37188/CO.2021-0220

冯维^{1, 2,,},
徐仕楠^{1, 2,},
王恒辉^{1, 2},
熊芝^{1, 2},
王选择^{1, 2},
翟中生^{1, 2}

1.
湖北工业大学机械工程学院, 武汉 430068
2.
现代制造质量工程湖北省重点实验室, 武汉 430068

基金项目:国家自然科学基金（No. 51805153）

详细信息

作者简介:
冯　维（1988—），男，湖北黄梅人，副教授，2011年、2014年于湖北工业大学分别获得学士、硕士学位，2018年于天津大学获得博士学位，主要从事光学三维测量与计算成像方面的研究。E-mail：fengwei@hbut.edu.cn
徐仕楠（1997—），男，湖北咸宁人，湖北工业大学硕士研究生，2019年于湖北工业大学获得学士学位，主要从事光学三维测量方面的研究。E-mail：101900018@hbut.edu.cn

中图分类号:TH741
计量
- 文章访问数:848
- HTML全文浏览量:436
- PDF下载量:211
- 被引次数:0
出版历程
- 收稿日期:2021-12-14
- 录用日期:2022-02-13
- 修回日期:2022-01-10
- 网络出版日期:2022-04-07
- 刊出日期:2022-05-20

Three-dimensional measurement method of highly reflective surface based on per-pixel modulation

FENG Wei^{1, 2,,},
XU Shi-nan^{1, 2,},
WANG Heng-hui^{1, 2},
XIONG Zhi^{1, 2},
WANG Xuan-ze^{1, 2},
ZHAI Zhong-sheng^{1, 2}

1.
School of Mechanical Engineering, Hubei University of Technology, Wuhan 430068, China
2.
Hubei Key Laboratory of Modern Manufacturing Quality Engineering, Wuhan 430068, China

Funds:Supported by National Natural Science Foundation of China (No. 51805153)

More Information

Corresponding author:fengwei@hbut.edu.cn

摘要

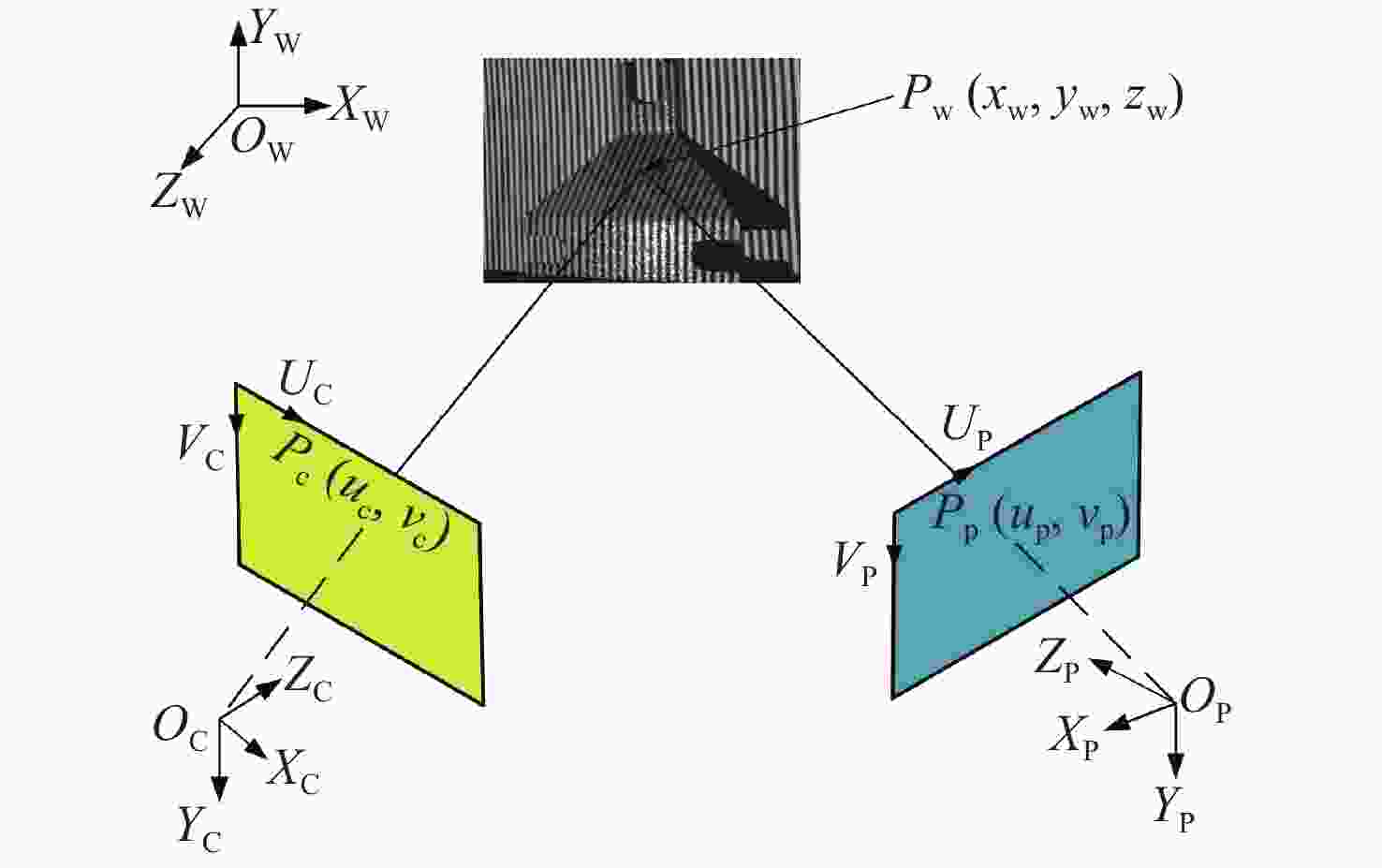
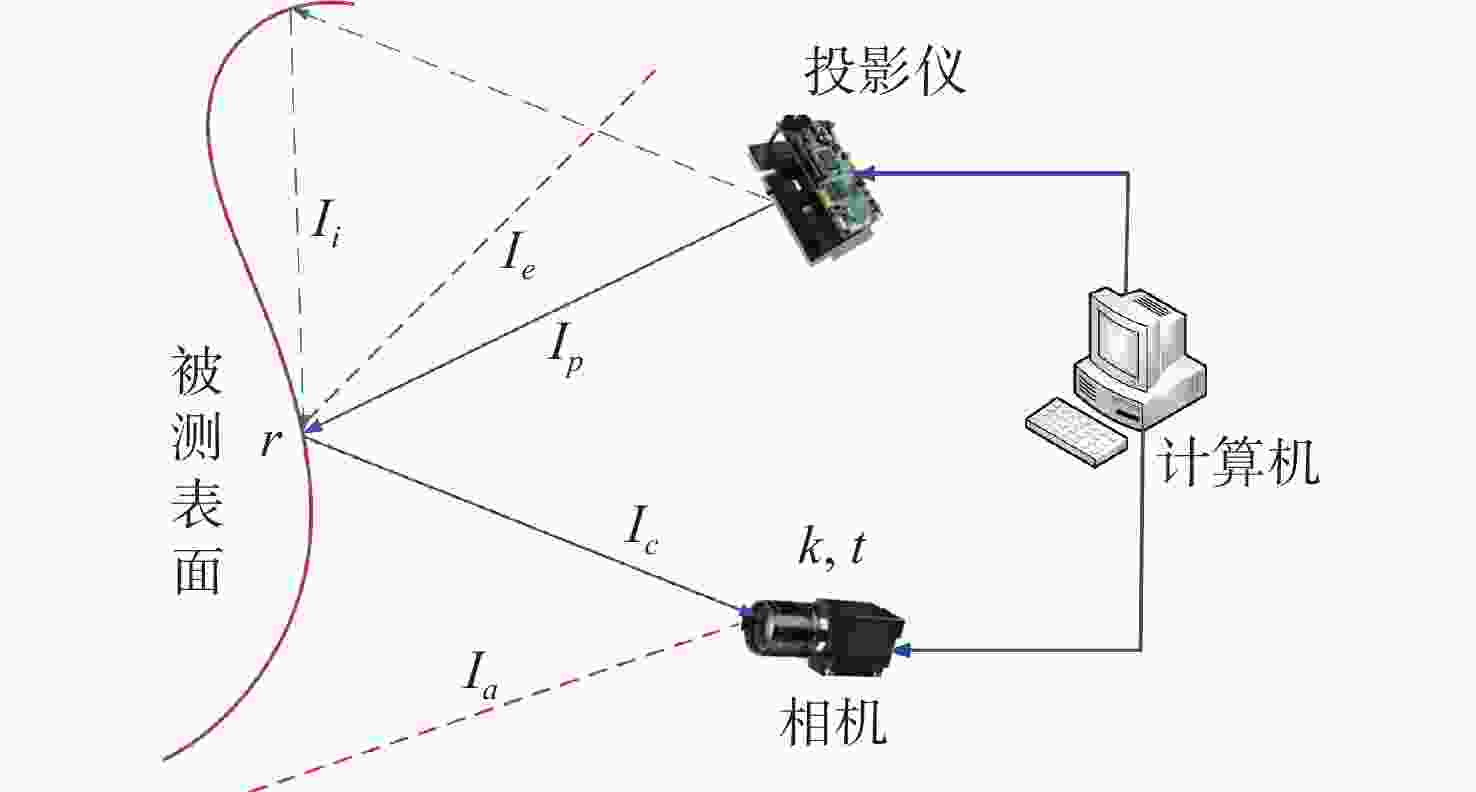
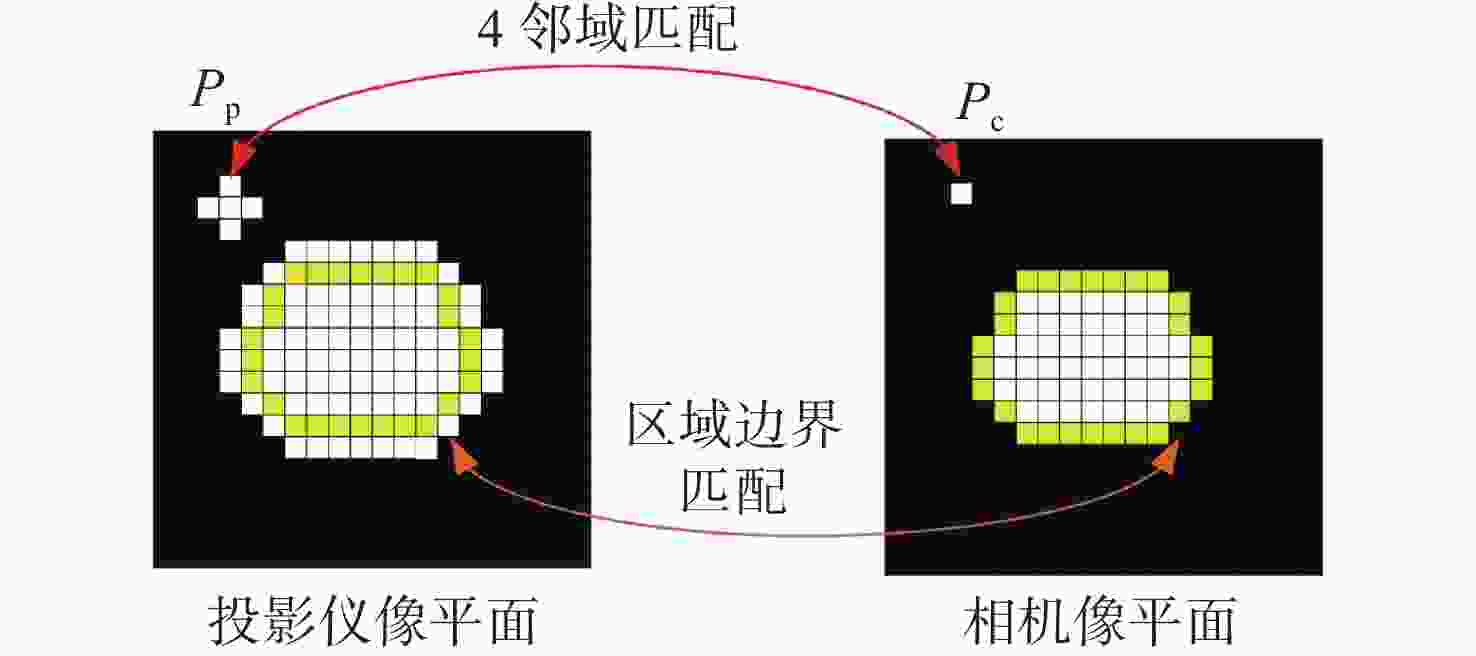
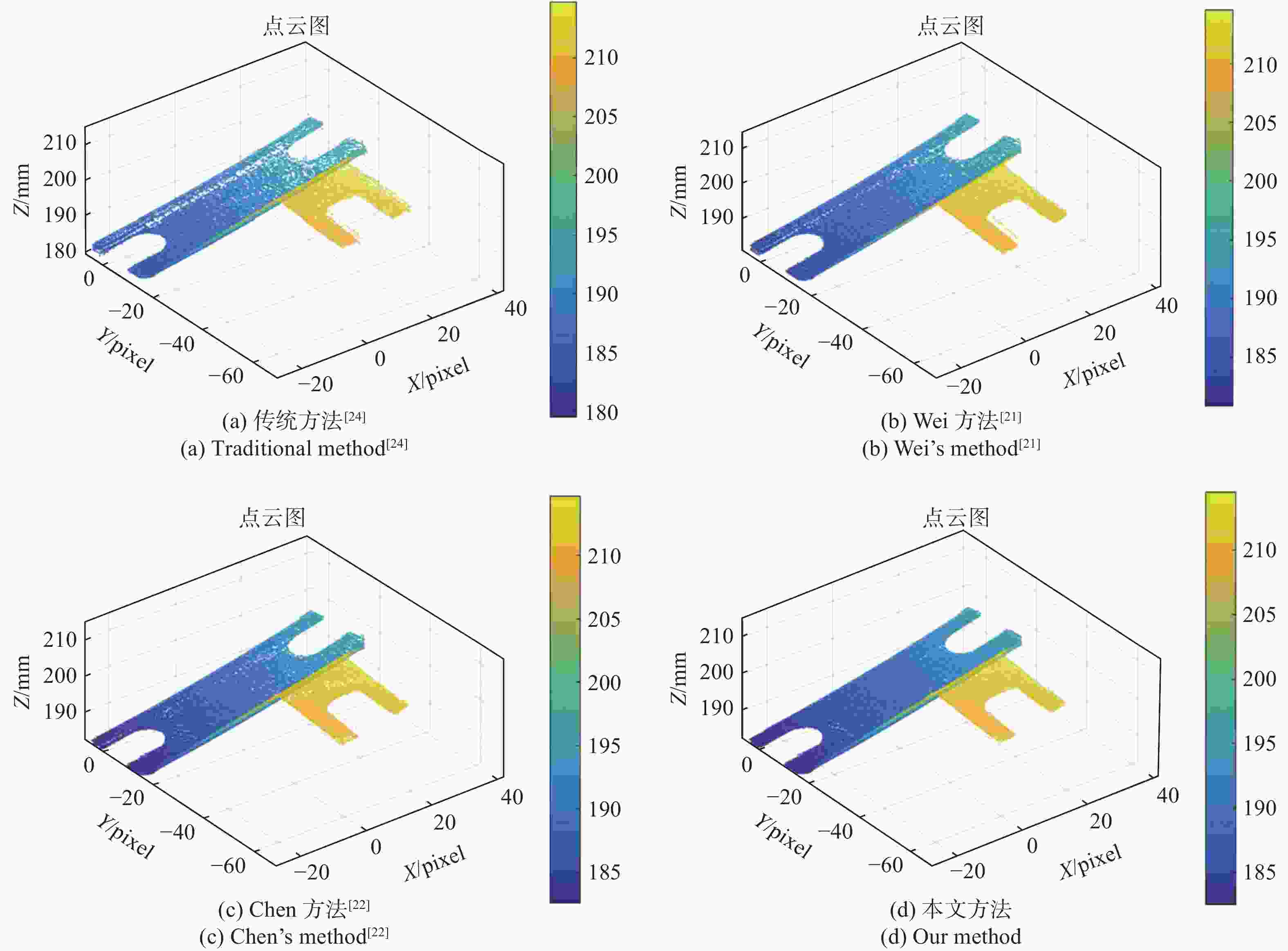
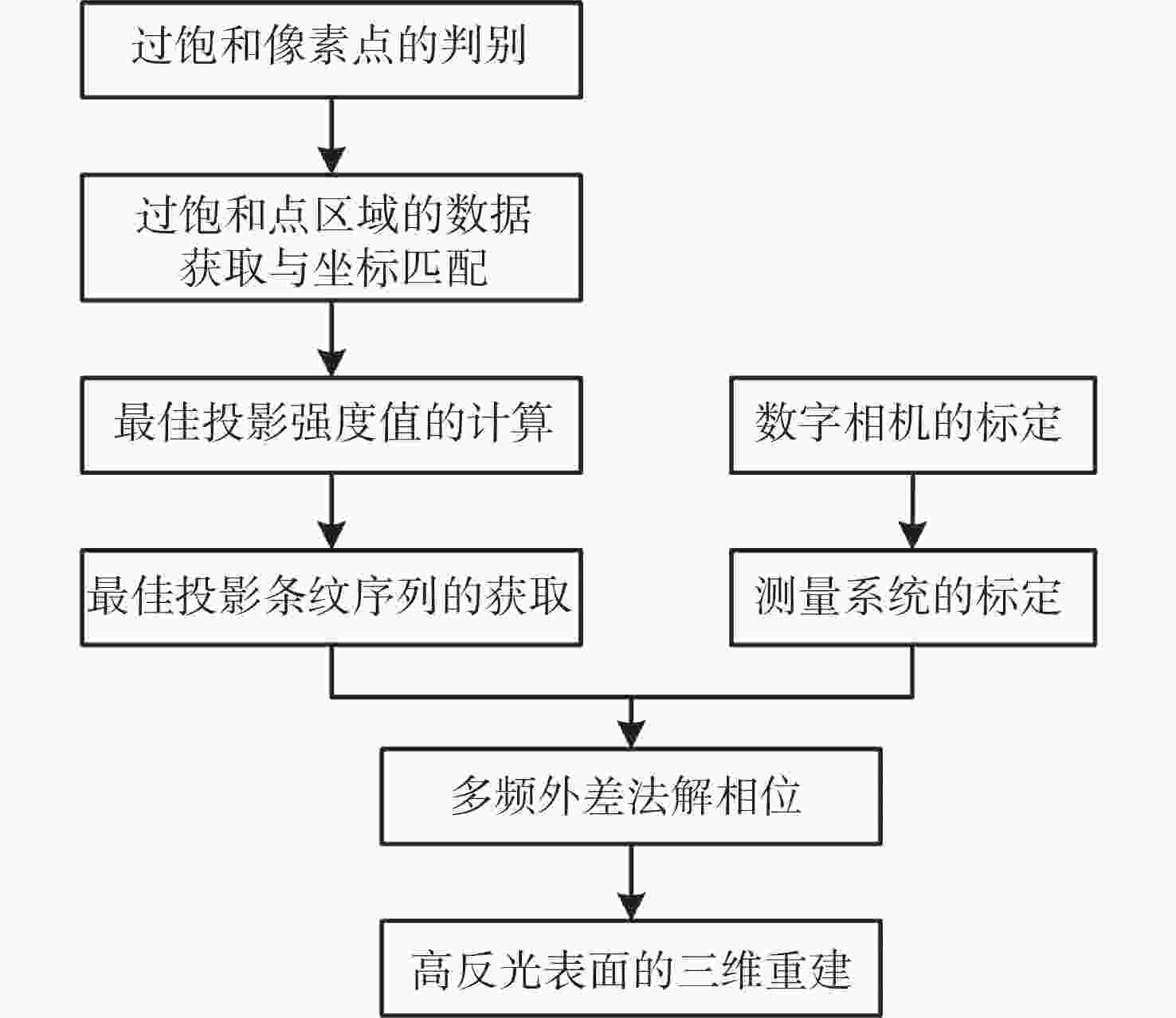
摘要:高反光表面的三维面形测量是光学三维测量领域的难题之一，本文提出一种基于逐像素调制的高反光表面三维测量方法，可解决光学三维测量中因过度曝光而导致的相位信息无法获取的问题。首先，通过投影最大灰度值的灰度图识别饱和像素点的位置；然后，依据投影低灰度下横纵条纹图进行过饱和区域坐标匹配，并结合一种新的相机-投影仪强度映射关系，逐像素求解过饱和像素点的最佳投影灰度值；最后，投影重新生成自适应条纹投影序列，并结合多频外差相移法用于相位恢复和三维重建。实验结果表明：所提方法的间距平均误差和标准偏差均小于文中其他方法所得的测量值，相对于传统方法，该方法的平均误差减少了61.9%，标准偏差减少了67.7%。本文所提方法的调制度高，速度快，能保证很高的测量精度。
- 三维测量/
- 逐像素调制/
- 高反光表面/
- 自适应条纹投影
Abstract:The three-dimensional (3D) shape measurement of highly reflective surface is one of the common problems in the field of optical 3D measurement. In this paper, a 3D measurement method of highly reflective surface based on per-pixel modulation was proposed to solve the problem that the phase information could not be obtained due to overexposure. Firstly, the positions of saturated pixels were identified by the projecting maximum gray image. Then, the coordinate matching was carried out by projecting horizontal and vertical fringes under low gray-level condition, and the optimal projecting gray value of supersaturated pixels would be per-pixel modulated by combining with a new intensity mapping relationship between camera and projector. Finally, the reconstructed and adaptive fringe projection sequences were projected, phase recovery and 3D reconstruction were realized by using the multi-frequency heterodyne phase shift method. The experimental results showed that the average error and standard deviation of the proposed method were less than the measured values obtained by other methods, and compared with the traditional method, the average error was reduced by 61.9% and the standard deviation was reduced by 67.7%. The proposed method has the advantages of high modulation, fast speed and can ensure high measurement accuracy.
- three-dimensional measurement/
- per-pixel modulation/
- highly reflective surface/
- adaptive fringe projection.

HTML全文

图 1自适应条纹三维测量方法流程图

Figure 1.Flow chart of adaptive fringe 3D measurement method

下载: 全尺寸图片幻灯片

图 2测量系统的坐标系示意图

Figure 2.Schematic diagram of coordinate of measurement system

下载: 全尺寸图片幻灯片

图 3被测表面反射光的组成

Figure 3.Composition of reflected light from the measured surface

下载: 全尺寸图片幻灯片

图 44邻域匹配法

Figure 4.Matching method based on 4 neighborhoods

下载: 全尺寸图片幻灯片

图 5三维测量系统实验平台

Figure 5.Experimental platform of 3D measurement system

下载: 全尺寸图片幻灯片

图 6阈值分割效果图

Figure 6.Threshold segmentation graph

下载: 全尺寸图片幻灯片

图 7相位展开流程图

Figure 7.Flow chart of phase unwrapping

下载: 全尺寸图片幻灯片

图 8自适应投影条纹图

Figure 8.Adaptive projection fringe image

下载: 全尺寸图片幻灯片

图 9（a）传统方法及（b）本文方法三维重建结果

Figure 9.3D reconstruction results obtained by (a) traditional method and (b) the proposed method

下载: 全尺寸图片幻灯片

图 10不同方法的三维重建结果

Figure 10.Experimental results of 3D reconstruction with different methods

下载: 全尺寸图片幻灯片

表 1本文方法与现有方法的误差检测结果

Table 1.Comparison of error detection results between the proposed method and existing methods

方法	过饱和像素点个数	有效补偿率	RMSE
传统方法^[24]	103756	0	4.3256
Wei方法^[21]	1356	98.69%	0.044
Chen方法^[22]	1023	99.01%	0.036
本文方法	856	99.17%	0.023

下载: 导出CSV

表 2本文方法与现有方法的误差对比分析

Table 2.Error analysis comparison between the proposed method and existing methods (mm)

方法	最大间距	最小间距	平均误差	标准偏差
传统方法^[24]	20.21	19.78	0.21	0.31
Wei方法^[21]	20.14	19.84	0.15	0.21
Chen方法^[22]	20.12	19.86	0.13	0.18
本文方法	20.08	19.92	0.08	0.10

下载: 导出CSV

参考文献 (24)

[1]	张宗华, 于瑾, 高楠, 等. 高反光表面三维形貌测量技术[J]. 红外与工程,2020,49(3):0303006.doi:10.3788/IRLA202049.0303006 ZHANG Z H, YU J, GAO N,et al. Three-dimensional shape measurement techniques of shiny surfaces[J].Infrared and Laser Engineering, 2020, 49(3): 0303006. (in Chinese)doi:10.3788/IRLA202049.0303006
[2]	曹智睿, 董吉洪. 结构光编码测量技术在火星高分相机中的应用[J]. 光学精密工程,2021,29(6):1420-1429.doi:10.37188/OPE.20212906.1420 CAO ZH R, DONG J H. Application of structured light coding measurement technology in Mars high-resolution camera[J].Optics and Precision Engineering, 2021, 29(6): 1420-1429. (in Chinese)doi:10.37188/OPE.20212906.1420
[3]	张宗华, 郭佼, 王月敏, 等. 镜面物体三维测量系统中两显示屏的平行正对校正[J]. 光学精密工程,2017,25(2):289-296.doi:10.3788/OPE.20172502.0289 ZHANG Z H, GUO J, WANG Y M,et al. Parallel-alignment and correction of two displays in three-dimensional measuring system of specular surfaces[J].Optics and Precision Engineering, 2017, 25(2): 289-296. (in Chinese)doi:10.3788/OPE.20172502.0289
[4]	王永红, 张倩, 胡寅, 等. 显微条纹投影小视场三维表面成像技术综述[J]. 中国光学,2021,14(3):447-457.doi:10.37188/CO.2020-0199 WANG Y H, ZHANG Q, HU Y,et al. 3D small-field surface imaging based on microscopic fringe projection profilometry: a review[J].Chinese Optics, 2021, 14(3): 447-457. (in Chinese)doi:10.37188/CO.2020-0199
[5]	马国庆, 刘丽, 于正林, 等. 大型复杂曲面三维形貌测量及应用研究进展[J]. 中国光学,2019,12(2):214-228.doi:10.3788/co.20191202.0214 MA G Q, LIU L, YU ZH L,et al. Application and development of three-dimensional profile measurement for large and complex surface[J].Chinese Optics, 2019, 12(2): 214-228. (in Chinese)doi:10.3788/co.20191202.0214
[6]	陈新禹, 孙非, 傅莉, 等. 相移光栅轮廓术的便携式三维测量系统[J]. 光学精密工程,2015,23(10):106-112. CHEN X Y, SUN F, FU L,et al. Phase shifting fringe profilometry based portable 3D measurement system[J].Optics and Precision Engineering, 2015, 23(10): 106-112. (in Chinese)
[7]	冯维, 汤少靖, 赵晓冬, 等. 基于自适应条纹的高反光表面三维面形测量方法[J]. 光学学报,2020,40(5):113-121. FENG W, TANG SH J, ZHAO X D,et al. Three-dimensional shape measurement method of high-reflective surfaces based on adaptive fringe-pattern[J].Acta Optica Sinica, 2020, 40(5): 113-121. (in Chinese)
[8]	FENG SH J, ZHANG Y ZH, CHEN Q,et al. General solution for high dynamic range three-dimensional shape measurement using the fringe projection technique[J].Optics and Lasers in Engineering, 2014, 59: 56-71.doi:10.1016/j.optlaseng.2014.03.003
[9]	ZHENG Y, WANG Y J, SURESH V,et al. Real-time high-dynamic-range fringe acquisition for 3D shape measurement with a RGB camera[J].Measurement Science and Technology, 2019, 30(7): 075202.doi:10.1088/1361-6501/ab0ced
[10]	LIANG R G. Short wavelength and polarized phase shifting fringe projection imaging of translucent objects[J].Optical Engineering, 2014, 53(1): 014104.doi:10.1117/1.OE.53.1.014104
[11]	郝婧蕾, 赵永强, 赵海盟, 等. 偏振多光谱机器视觉的高反光无纹理目标三维重构方法[J]. 测绘学报,2018,47(6):816-824.doi:10.11947/j.AGCS.2018.20170624 HAO J L, ZHAO Y Q, ZHAO H M,et al. 3D reconstruction of high-reflective and textureless targets based on multispectral polarization and machine vision[J].Acta Geodaetica et Cartographica Sinica, 2018, 47(6): 816-824. (in Chinese)doi:10.11947/j.AGCS.2018.20170624
[12]	WANG J H, ZHOU Y G, YANG Y X. A novel and fast three-dimensional measurement technology for the objects surface with non-uniform reflection[J].Results in Physics, 2020, 16: 102878.doi:10.1016/j.rinp.2019.102878
[13]	RAO L, DA F P. High dynamic range 3D shape determination based on automatic exposure selection[J].Journal of Visual Communication and Image Representation, 2017, 50: 217-226.
[14]	LIU Y ZH, FU Y J, CAI X Q,et al. A novel high dynamic range 3D measurement method based on adaptive fringe projection technique[J].Optics and Lasers in Engineering, 2020, 128: 106004.doi:10.1016/j.optlaseng.2020.106004
[15]	ZHAO X X, MO R, CHANG ZH Y,et al. 3D-design-model-assisted shiny surface shape measurement in fringe projection profilometry[J].Measurement Science and Technology, 2021, 32(3): 035019.doi:10.1088/1361-6501/abcc16
[16]	LIU Y ZH, FU Y J, ZHUAN Y H,et al. High dynamic range real-time 3D measurement based on Fourier transform profilometry[J].Optics&Laser Technology, 2021, 138: 106833.
[17]	LIN H, HAN ZH Q. Automatic optimal projected light intensity control for digital fringe projection technique[J].Optics Communications, 2021, 484: 126574.doi:10.1016/j.optcom.2020.126574
[18]	XU J, ZHANG S. Status, challenges, and future perspectives of fringe projection profilometry[J].Optics and Lasers in Engineering, 2020, 135: 106193.doi:10.1016/j.optlaseng.2020.106193
[19]	ZHANG S. Rapid and automatic optimal exposure control for digital fringe projection technique[J].Optics and Lasers in Engineering, 2020, 128: 106029.doi:10.1016/j.optlaseng.2020.106029
[20]	RIVIERE J, RESHETOUSKI I, FILIPI L,et al. Polarization imaging reflectometry in the wild[J].ACM Transactions on Graphics, 2017, 36(6): 206.
[21]	WEI Y F, LU L, XI J T,et al. 3D shape measurement of shiny surfaces based on optimized combination of fringe patterns of different intensity[J].Measurement Science and Technology, 2021, 32(3): 035203.doi:10.1088/1361-6501/abc49d
[22]	CHEN C, GAO N, WANG X J,et al. Adaptive projection intensity adjustment for avoiding saturation in three-dimensional shape measurement[J].Optics Communications, 2018, 410: 694-702.doi:10.1016/j.optcom.2017.11.009
[23]	LIU X H, HUANG SH J, ZHANG Z H,et al. Full-field calibration of color camera chromatic aberration using absolute phase maps[J].Sensors, 2017, 17(5): 1048.doi:10.3390/s17051048
[24]	盖绍彦, 达飞鹏. 一种新的相位法三维轮廓测量系统模型及其标定方法研究[J]. 自动化学报,2007,33(9):902-910. GAI S Y, DA F P. A new model of 3D shape measurement system based on phase measuring profilometry and its calibration[J].Acta Automatica Sinica, 2007, 33(9): 902-910. (in Chinese)