-
摘要:
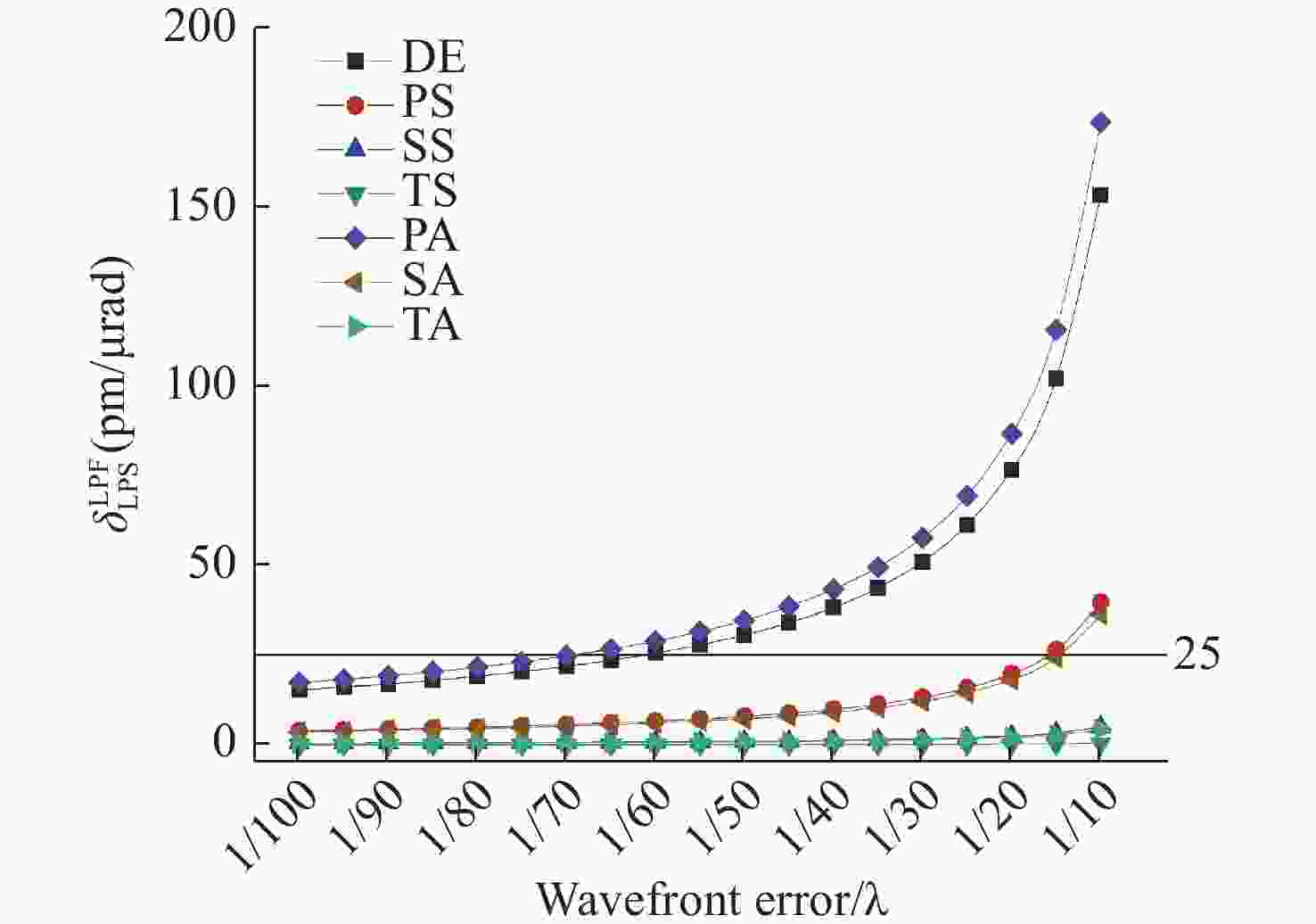
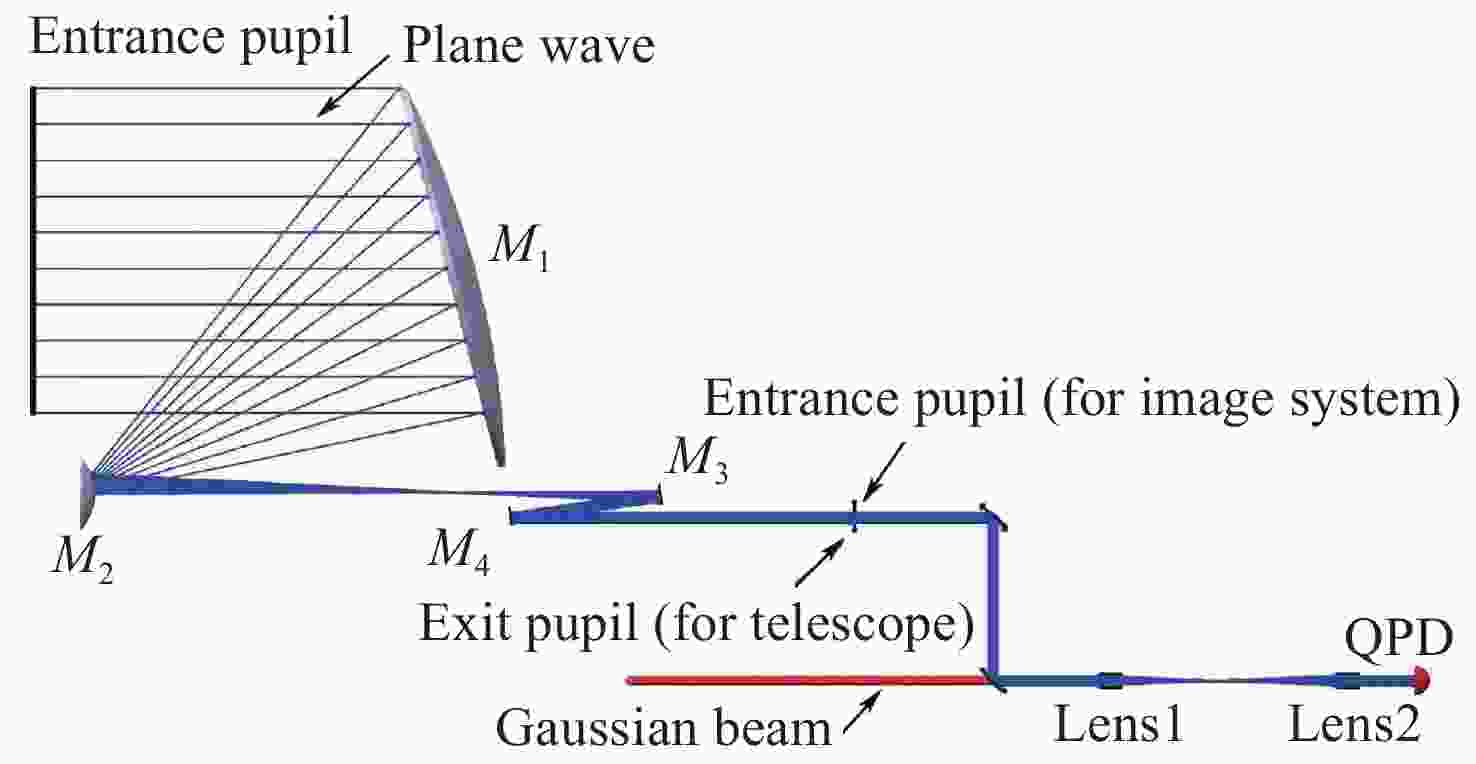
在空间引力波探测中，望远镜是空间 干涉测量系统的重要组成部分，其出瞳处波前误差与抖动光程(Tilt-To-Length, TTL)噪声间的耦合，是影响空间引力波探测的主要噪声源。首先，基于平顶光束与高斯光束的干涉模型，采用Fringe Zernike多项式表征望远镜出瞳处的波前误差，运用LISA Pathfinder(LPF)信号分析出瞳处波前误差与TTL噪声的耦合机理。其次，采用蒙特卡洛分析方法，研究不同数值波前误差下低阶像差占比对TTL耦合噪声的影响，确定了不同数值波前误差下，望远镜光学系统出瞳处满足TTL耦合噪声控制要求的低阶像差设计比例。最后，基于上述理论分析结果与像差控制要求，完成了空间引力波探测望远镜光学系统设计，望远镜入瞳直径为200 mm，出瞳处波前误差RMS值为0.01908λ，低阶像差占比不高于50%。分析结果表明，当光束抖动在±300 μrad以内，TTL耦合噪声不超过8.25 pm/μrad；通过公差分析得知，TTL耦合噪声最大值为15.50 pm/μrad，满足空间引力波的探测要求。
Abstract:In space gravitational wave detection, the telescope is an important part of the space laser interferometry system. The wavefront error at the exit pupil of the telescope is coupled with the Tilt-To-Length (TTL) noise, which becomes the main source of noise in space gravitational wave detection. Firstly, based on the interference model between a flat-top beam and a Gaussian beam, the Fringe Zernike polynomial is used to characterize the wavefront error at the exit pupil of the telescope, and the LISA Pathfinder (LPF) signal is used to analyze the coupling mechanism of the wavefront error at the exit pupil and the TTL noise. Secondly, the Monte Carlo analysis method is used to study the influence of the proportion of low-order aberrations on the TTL coupling noise under different numerical wavefront errors, and determine the low-order aberration proportions which meets the requirements of TTL coupling noise control at the exit pupil in the design of the telescope optical system under different numerical wavefront errors. Finally, based on the above theoretical analysis results and the aberration control requirements, the optical design of the space gravitational wave detection telescope is completed. The diameter of the entrance pupil of the telescope is 200 mm, and the RMS value of the wavefront error at the exit pupil is 0.01908λ. The proportion of low-order aberrations is not higher than 50%. The analysis results show that the TTL coupling noise does not exceed 8.25 pm/μrad when the beam jitter is within ±300 μrad. Through tolerance analysis, the maximum TTL coupling noise is determined to be 15.50 pm/μrad, which meets the requirements of space gravitational wave detection.
-
图 2干涉光束与四象限探测器的相对位置
Figure 2.The relative position of the interference beam and the four-quadrant detector
图 3倾斜像差余弦项与正弦项合并。（a）竖直倾斜项；（b）水平倾斜项；（c）合并后的倾斜项
Figure 3.Combined cosine and sine terms of the tilt aberration. (a) Vertical tilt aberration; (b) horizontal tilt aberration; (c) combined tilt aberration
图 4归一化的
${{\boldsymbol{M}}_{\mathbf{1}}}$ 和$ {{\boldsymbol{M}}_{\mathbf{2}}} $ 系数矩阵Figure 4.Normalized coefficients of the
$ {{\boldsymbol{M}}_{\mathbf{1}}} $ and$ {{\boldsymbol{M}}_{\mathbf{2}}} $ matrices
图 5
${{\boldsymbol{M}}_{\mathbf{2}}}$ 矩阵中不同像差对TTL噪声的影响Figure 5.The influence of different aberrations on TTL noise in the
$ {{\boldsymbol{M}}_{\mathbf{2}}} $ matrix
图 6低阶像差在不同占比下对TTL噪声的影响
Figure 6.The effect of low-order aberration on TTL noise under different proportions
图 8（a）优化后望远镜出瞳处波前；（b）TTL耦合噪声计算结果
Figure 8.(a) Wavefront at the exit pupil of the telescope after optimization; (b) calculation results of TTL coupled noise
图 9蒙特卡洛公差分析下耦合系数统计结果
Figure 9.Statistical results of coupling coefficient with Monte Carlo tolerance analysis
表 1由Fringe Zernike多项式的前25项组成的14个Zernike像差
Table 1.The fourteen Zernike aberrations consist of the first 25 terms of Fringe Zernike polynomials
i n, m j ${\textit{z}_j}\left( {\rho ,\theta } \right)$ Aberration Name 2,3 1,±1 1 ${\text{2} }\rho \cos (\theta - {\theta _{{\rm{TI}}} })$ Tilt (TI) 4 2,0 2 $ \sqrt 3 \left( {2{\rho ^2} - 1} \right) $ Defocus (DE) 5,6 2,±2 3 $\sqrt 6 {\rho ^2}\cos(2\theta - {\theta _{{\rm{PA}}} })$ Primary astigmatism (PA) 7,8 3,±1 4 $\sqrt 8 \left( {3{\rho ^2} - 2\rho } \right)\cos (\theta - {\theta _{{\rm{PC}}} })$ Primary coma (PC) 9 4,0 5 $ \sqrt 5 \left( {6{\rho ^4} - 6{\rho ^2} + 1} \right) $ Primary spherical (PS) 10,11 3,±3 6 $\sqrt 8 {\rho ^3}\cos(3\theta - {\theta _{{\rm{PTR}}} })$ Primary trefoil (PTR) 12,13 4,±2 7 $\sqrt {10} \left( {4{\rho ^4} - 3{\rho ^2} } \right)\cos (2\theta - {\theta _{{\rm{SA}}} })$ Secondary astigmatism (SA) 14,15 5,±1 8 $\sqrt {12} \left( {10{\rho ^5} - 12{\rho ^3} + 3\rho } \right)\cos (\theta - {\theta _{{\rm{SC}}} })$ Secondary coma (SC) 16 6,0 9 $ \sqrt 7 \left( {20{\rho ^6} - 30{\rho ^4} + 12{\rho ^2} - 1} \right) $ Secondary spherical (SS) 17,18 4,±4 10 $\sqrt {10} {\rho ^4}\cos(4\theta - {\theta _{{\rm{PTE}}} })$ Primary tetrafoil (PTE) 19,20 5,±3 11 $\sqrt {12} \left( {5{\rho ^5} - 4{\rho ^3} } \right)\cos (3\theta - {\theta _{{\rm{STR}}} })$ Secondary trefoil (STR) 21,22 6,±2 12 $\sqrt {14} \left( {15{\rho ^6} - 20{\rho ^4} + 6{\rho ^2} } \right)\cos (2\theta - {\theta _{{\rm{TA}}} })$ Tertiary astigmatism (TA) 23,24 7,±1 13 $4\left( {35{\rho ^7} - 60{\rho ^5} + 30{\rho ^3} - 3\rho } \right)\cos (2\theta - {\theta _{{\rm{TA}}} })$ Tertiary coma (TC) 25 8,0 14 $ 3\left( {70{\rho ^8} - 140{\rho ^6} + 90{\rho ^4} - 20{\rho ^2} + 1} \right) $ Tertiary spherical (TS) 
下载:
导出CSV
表 2不同占比低阶像差下TTL耦合噪声平均值及耦合噪声不超过25 pm/μrad的概率统计
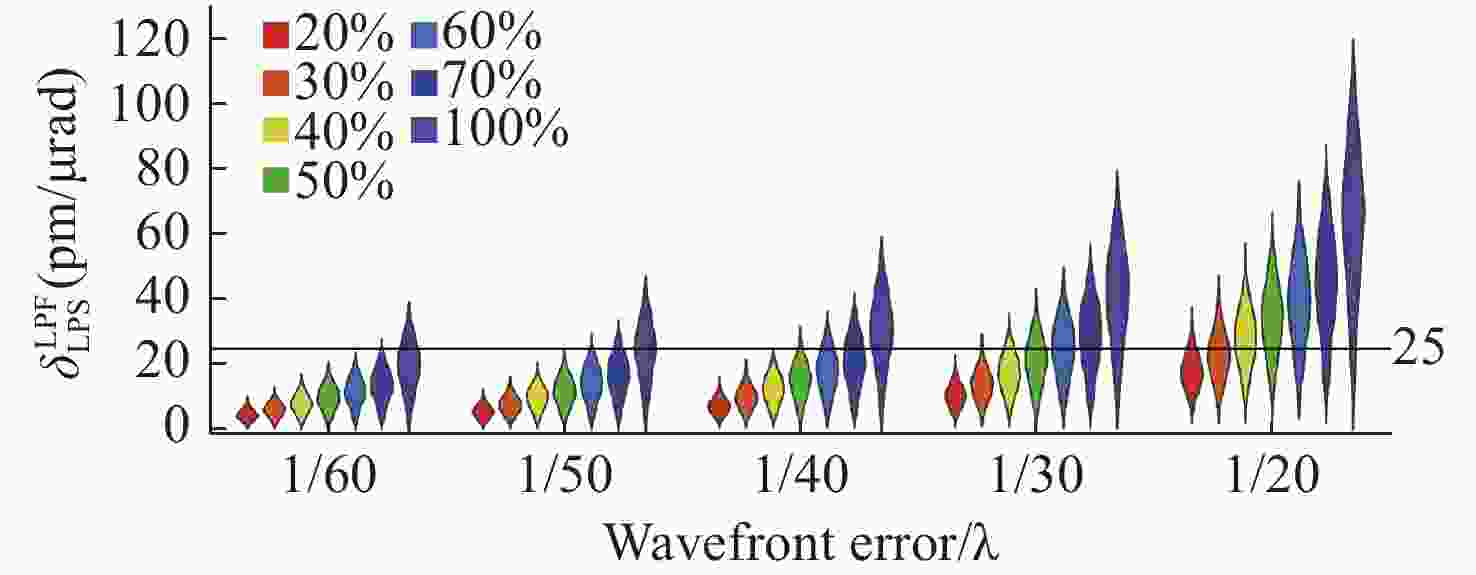
Table 2.Average value of TTL coupling noise and probability statistics for TTL coupling noise not exceeding 25 pm/μrad under different proportions of low-order aberrations
占比 λ/60 λ/50 λ/40 λ/30 λ/20 平均值 比例 平均值 比例 平均值 比例 平均值 比例 平均值 比例 20% 4.75 100.00% 5.85 100.00% 7.60 100.00% 10.76 100.00% 18.19 88.10% 30% 6.42 100.00% 7.86 100.00% 10.11 100.00% 14.15 98.92% 23.05 60.86% 40% 8.21 100.00% 10.07 100.00% 12.70 99.96% 17.62 88.50% 28.40 36.12% 50% 10.07 100.00% 11.98 100.00% 15.41 96.50% 21.23 68.92% 34.24 20.76% 60% 11.88 100.00% 14.51 98.54% 18.15 84.20% 25.16 48.26% 39.38 14.84% 70% 13.84 99.32% 16.78 90.80% 21.16 67.80% 29.03 34.62% 45.28 10.78% 100% 19.85 74.20% 24.32 50.98% 30.50 29.94% 41.52 14.30% 64.15 5.36% 下载:
导出CSV
表 3空间望远系统指标
Table 3.Indicators of space telescope system
系统参数 技术指标 入瞳直径/mm 200 工作波长/nm 1064 科学视场/μrad ±8 系统放大倍率 40 系统波像差 ≤ 0.03λ@1064 nm TTL耦合噪声 ≤ 25 pm/μrad 下载:
导出CSV
表 6Zernike多项式拟合望远镜出瞳处波前的幅值和方向
Table 6.Amplitude and orientation of the wavefront at the exit pupil of the telescope based on Zernike polynomials
Mag/Ori $A_2^{{\rm{DE}}}$ $A_3^{{\rm{PA}}}/{\theta _{ {\rm{PA} } } }$ $A_4^{{\rm{PC}}}/{\theta _{ {\rm{PC} } } }$ $ A_5^{{\rm{PS}}} $ $ A_6^{{\rm{PTR}}}/{\theta _{{\rm{PTR}}}} $ $ A_7^{{\rm{SA}}}/{\theta _{{\rm{SA}}}} $ $ A_8^{{\rm{SC}}}/{\theta _{{\rm{SC}}}} $ Value/(mm·rad−1) 1.30 3.74/3.14 3.93/4.71 1.15 4.52/4.71 2.08/3.14 8.36/1.57 Mag/Ori $ A_9^{{\rm{SS}}} $ $ A_{10}^{{\rm{PTE}}}/{\theta _{{\rm{PTE}}}} $ $ A_{11}^{{\rm{STR}}}/{\theta _{{\rm{STR}}}} $ $ A_{12}^{{\rm{TA}}}/{\theta _{{\rm{TA}}}} $ $ A_{13}^{{\rm{TC}}}/{\theta _{{\rm{TC}}}} $ $ A_{14}^{{\rm{TS}}} $ − Value/(mm·rad−1) 5.85 9.04/1.57 9.69/4.71 7.64/3.14 4.03/1.57 0.93 − 下载:
导出CSV
表 4优化后望远镜光学系统的设计参数
Table 4.Optimized design parameters of the telescope optical system
望远镜 曲率半径 空气间隔 圆锥系数 主镜 −1212.526 −573.883 −1.00537 次镜 −68.658 676.229 −1.36538 三镜 −760.425 −227.503 − 四镜 736.659 223.794 − 下载:
导出CSV
表 5次镜偶次非球面的高阶项系数
Table 5.High-order term coefficients of even-order aspheric surfaces of the secondary mirror
项数 4th 6th 8th 10th 12th 系数 2.9010×10−8 −1.2858×10−10 7.6057×10−12 5.8855×10−14 −4.5785×10−16 下载:
导出CSV
表 7望远镜公差分配
Table 7.Tolerance allocation of the telescope
类型 公差项 主镜 次镜 三镜 四镜 加工公差 曲率半径(mm) 0.1 0.02 0.1 0.1 二次曲面系数 0.0005 0.001 − − 面型精度(λ) 1/100 1/100 1/200 1/200 装调公差 X向位移(μm) − 15 20 20 Y向位移(μm) − 15 20 20 Z向位移(μm) − 15 20 20 绕X轴倾斜(″) − 20 20 20 绕Y轴倾斜(″) − 20 20 20 绕Z轴倾斜(″) − 40 60 60 下载:
导出CSV
-
[1] 罗子人, 白姗, 边星, 等. 空间 干涉引力波探测[J]. 力学进展,2013,43(4):415-447.doi:10.6052/1000-0992-13-044LUO Z R, BAI SH, BIAN X,et al. Gravitational wave detection by space laser interferometry[J].Advances in Mechanics, 2013, 43(4): 415-447. (in Chinese)doi:10.6052/1000-0992-13-044 [2] ABBOTT B P, ABBOTT R, ABBOTT T D,et al. Observation of gravitational waves from a binary black hole merger[J].Physical Review Letters, 2016, 116(6): 061102.doi:10.1103/PhysRevLett.116.061102 [3] 王智, 马军, 李静秋. 空间引力波探测计划-LISA系统设计要点[J]. 中国光学,2015,8(6):980-987.doi:10.3788/co.20150806.0980WANG ZH, MA J, LI J Q. Space-based gravitational wave detection mission: design highlights of LISA system[J].Chinese Optics, 2015, 8(6): 980-987. (in Chinese)doi:10.3788/co.20150806.0980 [4] 王璐钰, 李玉琼, 蔡榕. 空间 干涉仪 抖动噪声抑制研究[J]. 中国光学,2021,14(6):1426-1434.doi:10.37188/CO.2021-0045WANG L Y, LI Y Q, CAI R. Noise suppression of laser jitter in space laser interferometer[J].Chinese Optics, 2021, 14(6): 1426-1434. (in Chinese)doi:10.37188/CO.2021-0045 [5] 王登峰, 姚鑫, 焦仲科, 等. 面向天基引力波探测的时间延迟干涉技术[J]. 中国光学,2021,14(2):275-288.doi:10.37188/CO.2020-0098WANG D F, YAO X, JIAO ZH K,et al. Time-delay interferometry for space-based gravitational wave detection[J].Chinese Optics, 2021, 14(2): 275-288. (in Chinese)doi:10.37188/CO.2020-0098 [6] DANZMANN K, The LISA Study Team. LISA: laser interferometer space antenna for gravitational wave measurements[J].Classical and Quantum Gravity, 1996, 13(11A): A247-A250.doi:10.1088/0264-9381/13/11A/033 [7] LUO Z R, GUO Z K, JIN G,et al. A brief analysis to Taiji: science and technology[J].Results in Physics, 2020, 16: 102918.doi:10.1016/j.rinp.2019.102918 [8] LUO J, CHEN L SH, DUAN H Z,et al. TianQin: a space-borne gravitational wave detector[J].Classical and Quantum Gravity, 2016, 33(3): 035010.doi:10.1088/0264-9381/33/3/035010 [9] DONG Y H, LIU H SH, LUO Z R,et al. A comprehensive simulation of weak-light phase-locking for space-borne gravitational wave antenna[J].Science China Technological Sciences, 2016, 59(5): 730-737.doi:10.1007/s11431-016-6043-0 [10] CHWALLA M, DANZMANN K, BARRANCO G F,et al. Design and construction of an optical test bed for LISA imaging systems and tilt-to-length coupling[J].Classical and Quantum Gravity, 2016, 33(24): 245015.doi:10.1088/0264-9381/33/24/245015 [11] SUTTON A, MCKENZIE K, WARE B,et al. Laser ranging and communications for LISA[J].Optics Express, 2010, 18(20): 20759-20773.doi:10.1364/OE.18.020759 [12] SCHUSTER S, WANNER G, TRÖBS M,et al. Vanishing tilt-to-length coupling for a singular case in two-beam laser interferometers with Gaussian beams[J].Applied Optics, 2015, 54(5): 1010-1014.doi:10.1364/AO.54.001010 [13] SASSO C P, MANA G, MOTTINI S. Coupling of wavefront errors and pointing jitter in the LISA interferometer: misalignment of the interfering wavefronts[J].Classical and Quantum Gravity, 2018, 35(24): 245002.doi:10.1088/1361-6382/aaea0f [14] ZHAO Y, SHEN J, FANG CH,et al. Tilt-to-length noise coupled by wavefront errors in the interfering beams for the space measurement of gravitational waves[J].Optics Express, 2020, 28(17): 25545-25561.doi:10.1364/OE.397097 [15] ZHAO Y, SHEN J, FANG CH,et al. Far-field optical path noise coupled with the pointing jitter in the space measurement of gravitational waves[J].Applied Optics, 2021, 60(2): 438-444.doi:10.1364/AO.405467 [16] 王智, 沙巍, 陈哲, 等. 空间引力波探测望远镜初步设计与分析[J]. 中国光学,2018,11(1):131-151.doi:10.3788/co.20181101.0131WANG ZH, SHA W, CHEN ZH,et al. Preliminary design and analysis of telescope for space gravitational wave detection[J].Chinese Optics, 2018, 11(1): 131-151. (in Chinese)doi:10.3788/co.20181101.0131 [17] 李钰鹏, 王智, 沙巍, 等. 空间引力波望远镜主镜组件的结构设计[J]. 红外与 工程,2018,47(8):0818004.doi:10.3788/IRLA201847.0818004LI Y P, WANG ZH, SHA W,et al. Structural design of primary mirror subassembly for spatial gravitational wave telescope[J].Infrared and Laser Engineering, 2018, 47(8): 0818004. (in Chinese)doi:10.3788/IRLA201847.0818004 [18] 陈胜楠, 姜会林, 王春艳, 等. 大倍率离轴无焦四反光学系统设计[J]. 中国光学,2020,13(1):179-188.doi:10.3788/co.20201301.0179CHEN SH N, JIANG H L, WANG CH Y,et al. Design of off-axis four-mirror afocal optical system with high magnification[J].Chinese Optics, 2020, 13(1): 179-188. (in Chinese)doi:10.3788/co.20201301.0179 -
下载:
点击查看大图
计量
- 文章访问数:785
- HTML全文浏览量:304
- PDF下载量:222
- 被引次数:0
