-
摘要:
光学成像已成为跨尺度表征生物系统信息的主要方法之一，近年来生物样本的快速、无损且全面表征对成像系统的可解析量提出了更高的要求。数字全息通过干涉成像方式，可准确重构光波前的振幅和相位信息，具有快速、无损、三维成像等优势，在数字病理诊断、细胞无标记观察和实时监测等方面得到了广泛的研究和应用。本文首先介绍了实现高通量成像的主要方式，并分析了数字全息的优势及空间带宽变化，展示了基于希尔伯特变换的面向高通量多通道复用数字全息技术的理论框架，并介绍了基于该理论框架设计的拓展视场双通道复用数字全息显微成像系统。该系统在不牺牲空间和时间分辨率的情况下，可实现超越传统离轴全息显微镜8倍的空间带宽积。所介绍的数字全息复用技术可充分利用单幅强度图像的冗余空间带宽，可用于高通量多通道复用数字全息成像。
Abstract:Optical imaging has become the dominant method for characterizing information in biological systems. The rapid, non-destructive and comprehensive characterization of biological samples in recent years has placed high demands on the resolvable volume of imaging systems. Digital holography records an entire complex wavefront including both the amplitude and phase of the light field by interference imaging. Due to fast, non-destructive, and 3D imaging abilities, digital holography has been used in numerous applications such as digital pathology, label-free observation and real-time monitoring of in vitro cells. First, this paper introduces the main ways to achieve high-throughput imaging, and analyzes the advantages of digital holography and the evolution of spatial bandwidth. Secondly, a theoretical framework for high-throughput multi-channel multiplexing digital holography based on the Hilbert transform is presented. Then, an extended field of view digital holographic microscope is introduced based on this theoretical framework. Experimental results indicate that the system achieves 8 times the space-bandwidth product higher than that of conventional off-axis holographic microscopes without sacrificing spatial and temporal resolution. This high-throughput digital holographic multiplexing technology can make full use of the redundant spatial bandwidth of single intensity image, which verifies the feasibility of high-throughput multi-channel multiplexing digital holography.
-
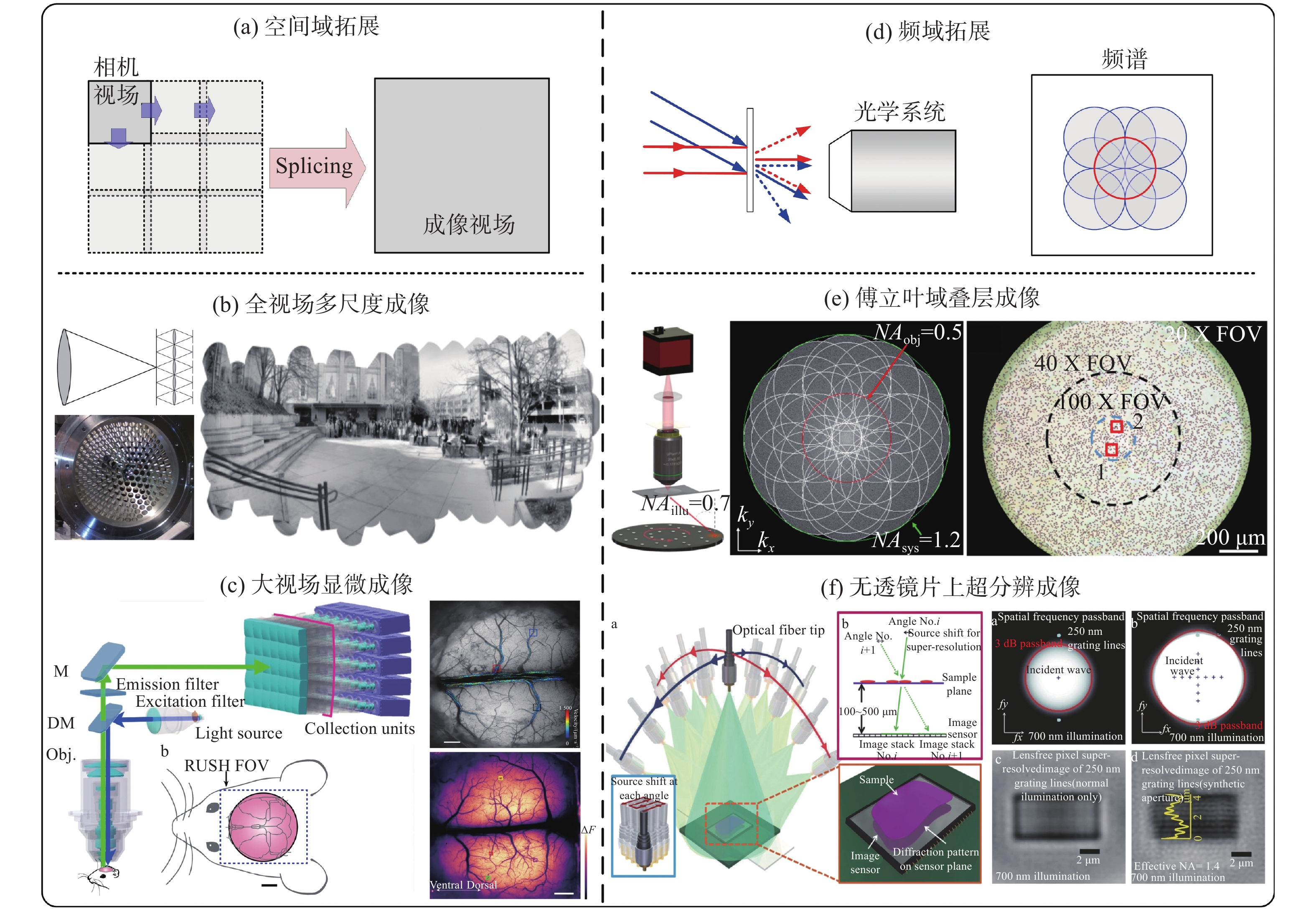
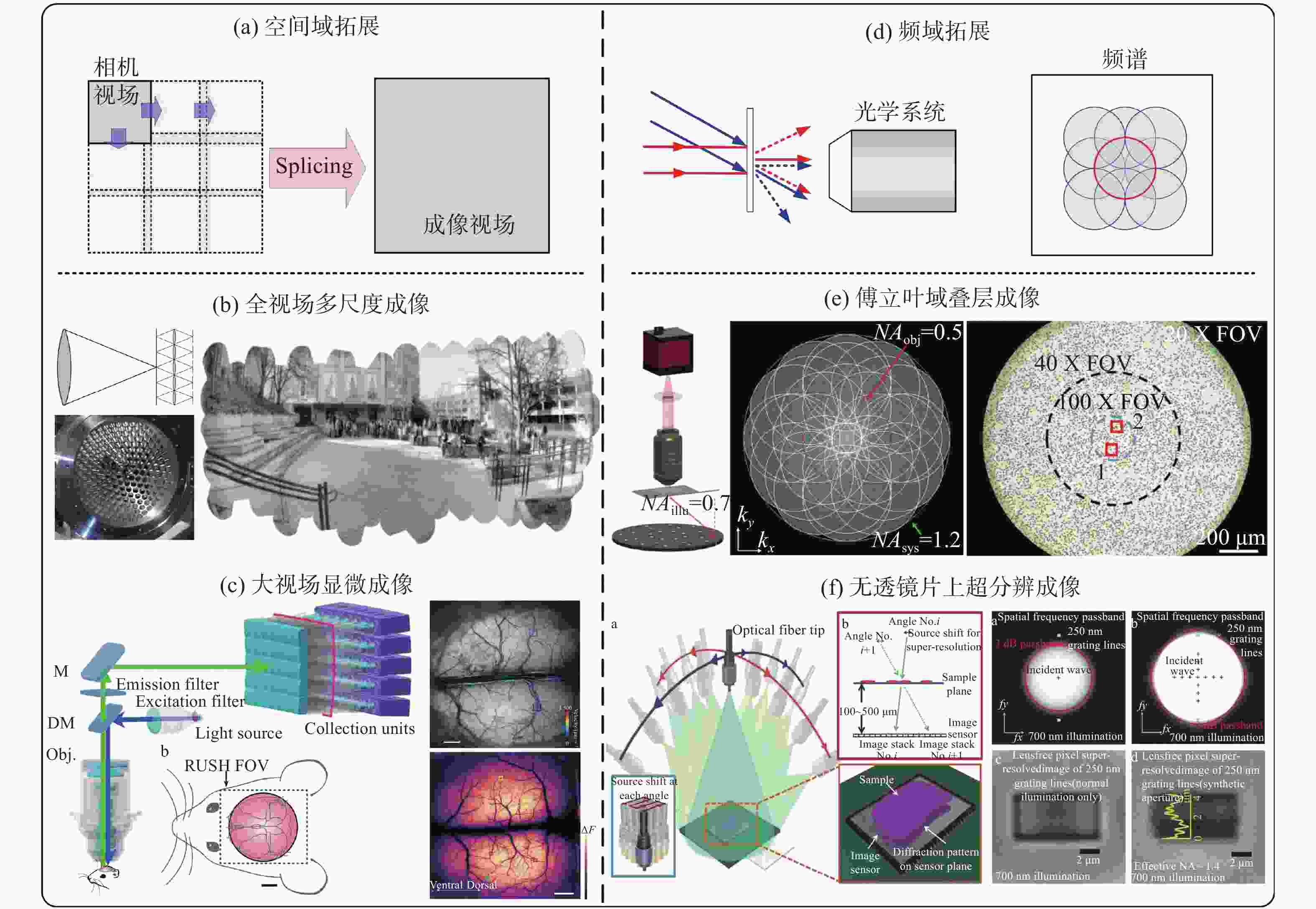
图 1 成像空间带宽积拓展。（a）空间域拓展示意，拓展光学系统的空间域成像范围；（b）基于相机阵列的多尺度光学成像系统[36-37]；（c）基于相机阵列的大视场生物显微成像系统[38]；（d）频域拓展示意，拓展现有光学系统的频率通带范围；（e）基于多角度照明的傅立叶域叠层显微成像系统[40]；（f）基于多角度照明的无透镜片上成像系统[41]。
Figure 1. The expansion of the imaging SBP. (a) Schematic diagram of the expansion in spatial domain to expand the spatial imaging range; (b) the multi-scale optical imaging system based on the camera array[36-37]; (c) the large field of view biological microscopic system based on the camera array[38]; (d) schematic diagram of frequency domain expansion, expanding the frequency passband range of existing optical systems; (e) fourier ptychographic microscopy system based on multi-angle illumination[40]; (f) lensless on-chip imaging systems based on multi-angle illumination[41]
图 2 传统离轴数字全息示意图，FT为傅里叶变换（Fourier transform）的简称
Figure 2. Schematic diagram of conventional off-axis digital holography. FT indicates the Fourier transform
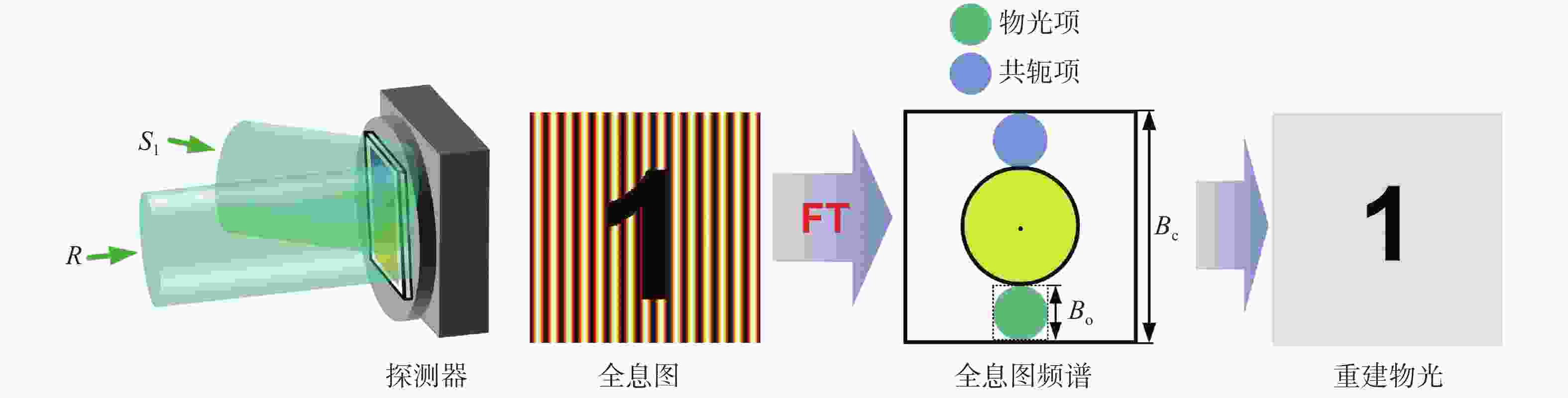
图 3 数字全息复用技术及其应用示意图。（a）双通道离轴全息复用示意图；（b）基于复用技术拓展成像视场[47]；（c）基于复用技术拓展成像分辨率[49]；（d）基于复用技术拓展成像深度[50]
Figure 3. Schematic diagram of digital holographic multiplexing and its applications. (a) Schematic diagram of dual-channel off-axis holographic multiplexing; (b) expanding imaging field of view based on digital holographic multiplexing[47]; (c) expanding imaging resolution based on digital holographic multiplexing[49]; (d) expanding imaging depth of field based on digital holographic multiplexing[50]
图 4 数值计算结果。（a）数字全息复用模型，以双通道为例；（b）～（c）2路原始物光相位分布；（d）2通道复用全息图的傅立叶频谱，物光谱与其他项完全分离；（e）～（f）对应（d）的2路重建物光相位分布；（g）2通道复用全息图的傅立叶频谱，物光谱与其他项重叠；（h）～（i）对应（g）2路重建物光相位分布；（j）8通道复用全息图的傅立叶频谱， 4路为物光1，其他4路为物光2，物光谱与其他项重叠；（k）～（l）对应（j）的其中2路重建物光相位分布
Figure 4. Numerical calculation results. (a) Digital holographic multiplexing model, taking two channels as an example; (b)～(c) phase distribution of original object; (d) fourier spectrum of the 2-channel multiplexed hologram, and the spectra are completely separated from other terms; (e)～(f) the reconstructed phases from (d); (g) fourier spectrum of the 2-channel multiplexed hologram, the object spectra are overlapped with other terms; (h)～(i) the reconstructed phases from (g); (j) fourier spectrum of 8-channel multiplexed hologram, 4 channels are the object 1, the other 4 channels are the object 2, and the object spectra are overlapped with other terms; (k)～(l) two of the reconstructed phases from (j)
图 5 数值计算结果。（a）相位重建MSE随采集位深变化的结果；（b）相位重建MSE随参考光振幅值变化的结果
Figure 5. Numerical calculation results. (a) The MSE result of phase reconstruction as a function of acquisition bit depth; (b) the MSE result of phase reconstruction as a function of the amplitude value of reference wave
图 6 高空间带宽利用率数字全息显微镜光路示意图。（a）视场拓展数字全息显微系统；（b）光路复用示意图；（c）视场复用示意图[48]
Figure 6. Schematic diagram of the optical path of a digital holographic microscope with high spatial bandwidth utilization. (a) Extended field-of-view digital holographic microscope; (b) schematic diagram of optical multiplexing setup; (c) schematic diagram of field-of-view multiplexing[48]
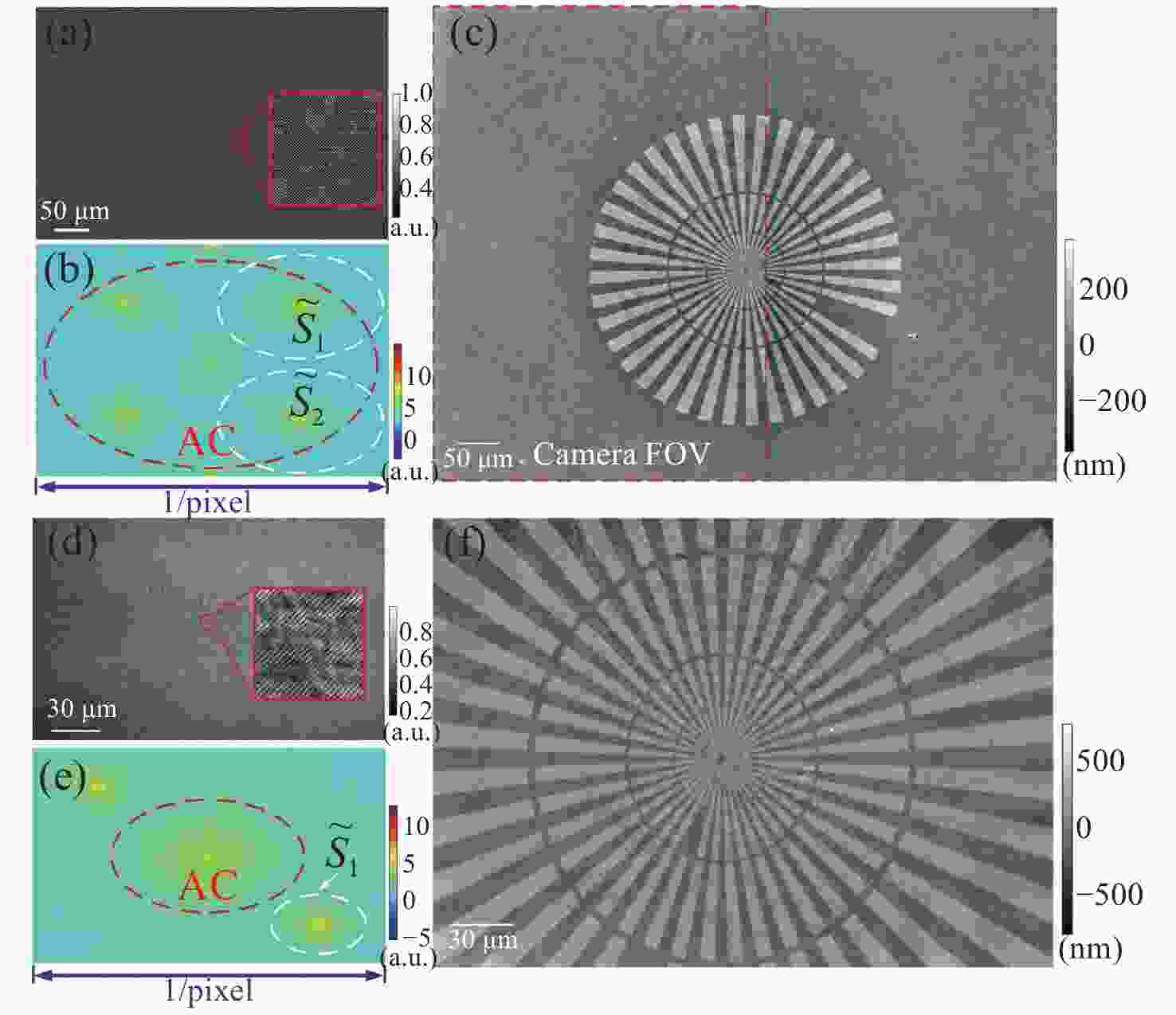
图 7 高空间带宽利用率数字全息显微镜重建图像[48]。（a）高通量复用全息图；（b）复用全息图的频谱；（c）高通量定量相位重建结果；（d）传统数字全息显微镜得到的全息图；（e）传统离轴全息频谱；（f）传统离轴全息重建结果
Figure 7. Reconstruction images from digital holographic microscope with high spatial bandwidth utilization[48]. (a) Multiplexed hologram; (b) spectrum of the multiplexed hologram; (c) high-throughput quantitative phase reconstruction from (a); (d) the hologram image obtained by conventional off-axis digital holographic microscope; (e) spectrum of conventional off-axis hologram; (f) the reconstruction results of conventional off-axis hologram in (d)
-
[1] GABOR D. A new microscopic principle[J]. Nature, 1948, 161(4098): 777-778. doi: 10.1038/161777a0 [2] HOEBE R A, VAN OVEN C H, GADELLA T W J JR, et al. Controlled light-exposure microscopy reduces photobleaching and phototoxicity in fluorescence live-cell imaging[J]. Nature Biotechnology, 2007, 25(2): 249-253. doi: 10.1038/nbt1278 [3] GORDON M P, HA T, SELVIN P R. Single-molecule high-resolution imaging with photobleaching[J]. Proceedings of the National Academy of Sciences of the United States of America, 2004, 101(17): 6462-6465. doi: 10.1073/pnas.0401638101 [4] ZERNIKE F. Phase contrast, a new method for the microscopic observation of transparent objects[J]. Physica, 1942, 9(7): 686-698. doi: 10.1016/S0031-8914(42)80035-X [5] NOMARSKI G M. Differential microinterferometer with polarized waves[J]. Journal de Physique et le Radium, 1955, 16: 9s-13s. [6] ZUO J M, VARTANYANTS I, GAO M, et al. Atomic resolution imaging of a carbon nanotube from diffraction intensities[J]. Science, 2003, 300(5624): 1419-1421. doi: 10.1126/science.1083887 [7] ZHANG F C, CHEN B, MORRISON G R, et al. Phase retrieval by coherent modulation imaging[J]. Nature Communications, 2016, 7(1): 13367. doi: 10.1038/ncomms13367 [8] ZUO CH, LI J J, SUN J S, et al. Transport of intensity equation: a tutorial[J]. Optics and Lasers in Engineering, 2020, 135: 106187. doi: 10.1016/j.optlaseng.2020.106187 [9] ZUO CH, CHEN Q, ASUNDI A. Boundary-artifact-free phase retrieval with the transport of intensity equation: fast solution with use of discrete cosine transform[J]. Optics Express, 2014, 22(8): 9220-9244. doi: 10.1364/OE.22.009220 [10] WALLER L, TIAN L, BARBASTATHIS G. Transport of Intensity phase-amplitude imaging with higher order intensity derivatives[J]. Optics Express, 2010, 18(12): 12552-12561. doi: 10.1364/OE.18.012552 [11] FAULKNER H M L, RODENBURG J M. Movable aperture lensless transmission microscopy: a novel phase retrieval algorithm[J]. Physical Review Letters, 2004, 93(2): 023903. doi: 10.1103/PhysRevLett.93.023903 [12] RODENBURG J M, FAULKNER H M L. A phase retrieval algorithm for shifting illumination[J]. Applied Physics Letters, 2004, 85(20): 4795-4797. doi: 10.1063/1.1823034 [13] ZHENG G A, HORSTMEYER R, YANG C. Wide-field, high-resolution Fourier ptychographic microscopy[J]. Nature Photonics, 2013, 7(9): 739-745. doi: 10.1038/nphoton.2013.187 [14] WU J CH, YANG F, CAO L C. Resolution enhancement of long-range imaging with sparse apertures[J]. Optics and Lasers in Engineering, 2022, 155: 107068. doi: 10.1016/j.optlaseng.2022.107068 [15] 孙佳嵩, 张玉珍, 陈钱, 等. 傅里叶叠层显微成像技术: 理论、发展和应用[J]. 光学学报,2016,36(10):1011005. doi: 10.3788/AOS201636.1011005SUN J S, ZHANG Y ZH, CHEN Q, et al. Fourier ptychographic microscopy: theory, advances, and applications[J]. Acta Optica Sinica, 2016, 36(10): 1011005. (in Chinese) doi: 10.3788/AOS201636.1011005 [16] 潘安, 张艳, 赵天宇, 等. 基于叠层衍射成像术的量化相位显微成像[J]. 与光电子学进展,2017,54(4):040001.PAN A, ZHANG Y, ZHAO T Y, et al. Quantitative phase microscopy imaging based on ptychography[J]. Laser &Optoelectronics Progress, 2017, 54(4): 040001. (in Chinese) [17] 张韶辉, 周国城, 崔柏岐, 等. 傅里叶叠层显微成像模型、算法及系统研究综述[J]. 与光电子学进展,2021,58(14):1400001.ZHANG SH H, ZHOU G CH, CUI B Q, et al. Review of fourier ptychographic microscopy: models, algorithms, and systems[J]. Laser &Optoelectronics Progress, 2021, 58(14): 1400001. (in Chinese) [18] BAEK Y S, PARK Y K. Intensity-based holographic imaging via space-domain Kramers–Kronig relations[J]. Nature Photonics, 2021, 15(5): 354-360. doi: 10.1038/s41566-021-00760-8 [19] SHEN CH, LIANG M SH, PAN A, et al. Non-iterative complex wave-field reconstruction based on Kramers–Kronig relations[J]. Photonics Research, 2021, 9(6): 1003-1012. doi: 10.1364/PRJ.419886 [20] LEE C, BAEK Y, HUGONNET H, et al. Single-shot wide-field topography measurement using spectrally multiplexed reflection intensity holography via space-domain Kramers–Kronig relations[J]. Optics Letters, 2022, 47(5): 1025-1028. doi: 10.1364/OL.446159 [21] PARK Y K, DEPEURSINGE C, POPESCU G. Quantitative phase imaging in biomedicine[J]. Nature Photonics, 2018, 12(10): 578-589. doi: 10.1038/s41566-018-0253-x [22] YAMAGUCHI I, ZHANG T. Phase-shifting digital holography[J]. Optics Letters, 1997, 22(16): 1268-1270. doi: 10.1364/OL.22.001268 [23] AWATSUJI Y, SASADA M, KUBOTA T. Parallel quasi-phase-shifting digital holography[J]. Applied Physics Letters, 2004, 85(6): 1069-1071. doi: 10.1063/1.1777796 [24] AWATSUJI Y, FUJII A, KUBOTA T, et al. Parallel three-step phase-shifting digital holography[J]. Applied Optics, 2006, 45(13): 2995-3002. doi: 10.1364/AO.45.002995 [25] AWATSUJI Y, TAHARA T, KANEKO A, et al. Parallel two-step phase-shifting digital holography[J]. Applied Optics, 2008, 47(19): D183-D189. doi: 10.1364/AO.47.00D183 [26] LOHMANN A W. Reconstruction of vectorial wavefronts[J]. Applied Optics, 1965, 4(12): 1667-1668. doi: 10.1364/AO.4.001667 [27] 王云新, 王大勇, 杨怡姝, 等. 数字全息技术在生物医学成像和分析中的应用[J]. 中国 ,2014,41(2):0209002. doi: 10.3788/CJL201441.0209002WANG Y X, WANG D Y, YANG Y SH, et al. Application and analysis in the biomedicine field using digital holographic technology[J]. Chinese Journal of Lasers, 2014, 41(2): 0209002. (in Chinese) doi: 10.3788/CJL201441.0209002 [28] HUANG ZH ZH, MEMMOLO P, FERRARO P, et al. Dual-plane coupled phase retrieval for non-prior holographic imaging[J]. PhotoniX, 2022, 3(1): 3. doi: 10.1186/s43074-021-00046-w [29] PARK J, BRADY D, ZHENG G A, et al. Review of bio-optical imaging systems with a high space-bandwidth product[J]. Advanced Photonics, 2021, 3(4): 044001. [30] BIAN Z CH, GUO CH F, JIANG SH W, et al. Autofocusing technologies for whole slide imaging and automated microscopy[J]. Journal of Biophotonics, 2020, 13(12): e202000227. [31] AL-JANABI S, HUISMAN A, VAN DIEST P J. Digital pathology: current status and future perspectives[J]. Histopathology, 2012, 61(1): 1-9. doi: 10.1111/j.1365-2559.2011.03814.x [32] FARAHANI N, PARWANI A, PANTANOWITZ L. Whole slide imaging in pathology: advantages, limitations, and emerging perspectives[J]. Pathology and Laboratory Medicine International, 2015, 7: 23-33. [33] BARISONI L, LAFATA K J, HEWITT S M, et al. Digital pathology and computational image analysis in nephropathology[J]. Nature Reviews Nephrology, 2020, 16(11): 669-685. doi: 10.1038/s41581-020-0321-6 [34] HUGONNET H, KIM Y W, LEE M, et al. Multiscale label-free volumetric holographic histopathology of thick-tissue slides with subcellular resolution[J]. Advanced Photonics, 2021, 3(2): 026004. [35] BRADY D J, GEHM M E, STACK R A, et al. Multiscale gigapixel photography[J]. Nature, 2012, 486(7403): 386-389. doi: 10.1038/nature11150 [36] BRADY D J, HAGEN N. Multiscale lens design[J]. Optics Express, 2009, 17(13): 10659-10674. doi: 10.1364/OE.17.010659 [37] GOLISH D R, VERA E M, KELLY K J, et al. Development of a scalable image formation pipeline for multiscale gigapixel photography[J]. Optics Express, 2012, 20(20): 22048-22062. doi: 10.1364/OE.20.022048 [38] FAN J T, SUO J L, WU J M, et al. Video-rate imaging of biological dynamics at centimetre scale and micrometre resolution[J]. Nature Photonics, 2019, 13(11): 809-816. doi: 10.1038/s41566-019-0474-7 [39] OU X Z, HORSTMEYER R, YANG C, et al. Quantitative phase imaging via Fourier ptychographic microscopy[J]. Optics Letters, 2013, 38(22): 4845-4848. doi: 10.1364/OL.38.004845 [40] OU X Z, HORSTMEYER R, ZHENG G A, et al. High numerical aperture Fourier ptychography: principle, implementation and characterization[J]. Optics Express, 2015, 23(3): 3472-3491. doi: 10.1364/OE.23.003472 [41] LUO W, GREENBAUM A, ZHANG Y B, et al. Synthetic aperture-based on-chip microscopy[J]. Light:Science &Applications, 2015, 4(3): e261. [42] ISIKMAN S O, BISHARA W, MAVANDADI S, et al. Lens-free optical tomographic microscope with a large imaging volume on a chip[J]. Proceedings of the National Academy of Sciences of the United States of America, 2011, 108(18): 7296-7301. doi: 10.1073/pnas.1015638108 [43] MICÓ V, ZHENG J J, GARCIA J, et al. Resolution enhancement in quantitative phase microscopy[J]. Advances in Optics and Photonics, 2019, 11(1): 135-214. doi: 10.1364/AOP.11.000135 [44] GAO P, YUAN C J. Resolution enhancement of digital holographic microscopy via synthetic aperture: a review[J]. Light:Advanced Manufacturing, 2022, 3: 6. [45] SHAKED N T, MICÓ V, TRUSIAK M, et al. Off-axis digital holographic multiplexing for rapid wavefront acquisition and processing[J]. Advances in Optics and Photonics, 2020, 12(3): 556-611. doi: 10.1364/AOP.384612 [46] DARDIKMAN G, SHAKED N T. Is multiplexed off-axis holography for quantitative phase imaging more spatial bandwidth-efficient than on-axis holography? [Invited][J]. Journal of the Optical Society of America A, 2019, 36(2): A1-A11. doi: 10.1364/JOSAA.36.0000A1 [47] GIRSHOVITZ P, SHAKED N T. Doubling the field of view in off-axis low-coherence interferometric imaging[J]. Light:Science &Applications, 2014, 3(3): e151. [48] HUANG ZH ZH, CAO L C. High bandwidth-utilization digital holographic multiplexing: an approach using Kramers–Kronig relations[J]. Advanced Photonics Research, 2022, 3(2): 2100273. doi: 10.1002/adpr.202100273 [49] MIRSKY S K, SHAKED N T. First experimental realization of six-pack holography and its application to dynamic synthetic aperture superresolution[J]. Optics Express, 2019, 27(19): 26708-26720. doi: 10.1364/OE.27.026708 [50] WOLBROMSKY L, TURKO N A, SHAKED N T. Single-exposure full-field multi-depth imaging using low-coherence holographic multiplexing[J]. Optics Letters, 2018, 43(9): 2046-2049. doi: 10.1364/OL.43.002046 [51] DARDIKMAN G, TURKO N A, NATIV N, et al. Optimal spatial bandwidth capacity in multiplexed off-axis holography for rapid quantitative phase reconstruction and visualization[J]. Optics Express, 2017, 25(26): 33400-33415. doi: 10.1364/OE.25.033400 [52] MARPLE S L. Computing the discrete-time "analytic" signal via FFT[J]. IEEE Transactions on Signal Processing, 1999, 47(9): 2600-2603. doi: 10.1109/78.782222 [53] BAEK Y S, LEE K R, SHIN S, et al. Kramers–Kronig holographic imaging for high-space-bandwidth product[J]. Optica, 2019, 6(1): 45-51. doi: 10.1364/OPTICA.6.000045 [54] FRENKLACH I, GIRSHOVITZ P, SHAKED N T. Off-axis interferometric phase microscopy with tripled imaging area[J]. Optics Letters, 2014, 39(6): 1525-1528. doi: 10.1364/OL.39.001525 -
下载:
计量
- 文章访问数: 1960
- HTML全文浏览量: 1049
- PDF下载量: 739
- 被引次数: 0
