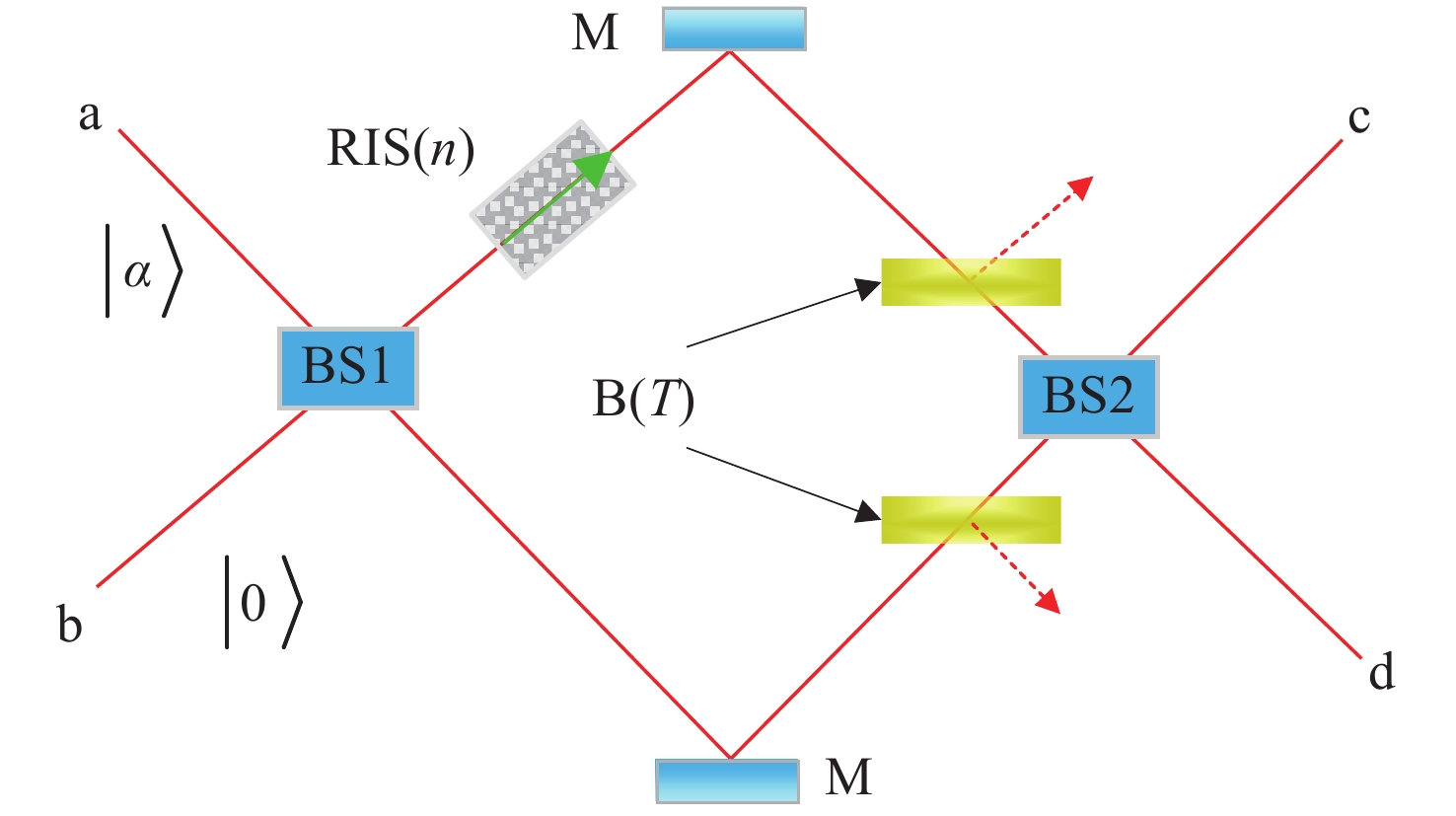
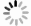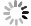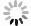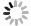Theoretical investigation on super-resolution refractive index measurement with parity detection
doi:10.37188/CO.2022-0119
-
摘要:
传统波动光学法测量样品折射率所采用的探测方法主要是强度探测和波长探测。波长的最佳检测器件为干涉型光谱仪，干涉型光谱仪是通过光功率计测量信号强度、分析条纹数目变化及所对应的光程差，进而计算出信号光波长，因此，其本质仍是以强度探测为基础的。然而，利用强度探测干涉信号，分辨率受经典衍射极限限制，很难得到进一步提升。为了解决这一瓶颈问题，本文提出利用奇偶探测突破经典分辨率的极限限制，实现超分辨率折射率测量。根据量子探测与估计理论，推导了奇偶探测和强度探测折射率测量信号及其灵敏度表达式，并进行了数值对比分析。同时，研究了损耗对系统输出信号分辨率和灵敏度的影响。数值结果表明：奇偶探测分辨率是强度探测的
${\text{2{\text{π}}}}\sqrt {{N}} $ 倍，实现了超分辨率折射率测量，最佳灵敏度达到了折射率测量散弹噪声极限${\lambda / {\left( {2{\text{π}} l\sqrt N } \right)}}$ ，损耗降低了信号的分辨率和灵敏度，除极大损耗和极低光子数外，奇偶探测信号分辨率始终优于强度探测。最后，从探测手段本身出发分析了奇偶探测超分辨率折射率测量的物理本质。Abstract:The refractive index measurements based on traditional wave optical methods are mainly depended on intensity and wavelength detection strategies. Interference spectrometers are widely used as the most ideal wavelength detecting devices. Interference spectrometers measure the signal intensity, analyze the change of fringe numbers and the corresponding optical path difference by means of optical power meter, and then calculate the wavelength of signal light. Therefore, its essence is still based on intensity detection. However, the resolution of interference signal in intensity detection is restricted by classical diffraction limit, thus its resolution is difficult to further improve. In order to solve this bottleneck, parity detection which could break through the classical resolution limit and realize super-resolution refractive index measurement is proposed in this paper. According to the quantum detection and estimation theory, the expressions for signals and their corresponding sensitivities of refractive index measurement with parity and intensity detections were derived respectively and their numerical comparison analysis was carried out. In addition, the effects of loss on resolution and sensitivity of the output signal were investigated. Numerical results show that the resolution of parity detection is
${\text{2{\text{π}}}}\sqrt N$ times that of intensity detection, achieving super-resolution refractive index measurement. Moreover, the optimal sensitivity reaches the refractive index measurement shot noise limit${\lambda \mathord{\left/ {\vphantom {\lambda {\left( {2{\text{π}} l\sqrt N } \right)}}} \right. } {\left( {2{\text{π}} l\sqrt N } \right)}}$ . The loss reduces the sensitivity and resolution of the signal. The resolution of the parity detection signal is consistently better than that of intensity detection except for the very large loss and very low photon number. Finally, the physical essence of the super-resolution refractive index measurement is analyzed from the detection means itself. -
图 1奇偶探测超分辨率折射率测量原理示意图
Figure 1.Schematic diagram of super-resolution refractive index measurement principle using parity detection
图 2(a) 强度探测折射率测量灵敏度曲线及(b)信号最佳灵敏度随光子数和透过率的变化关系
Figure 2.(a) Sensitivity curve of intensity-detection-based refractive index measurement and (b) signal optimal sensitivity as a function of photon number and transmittance
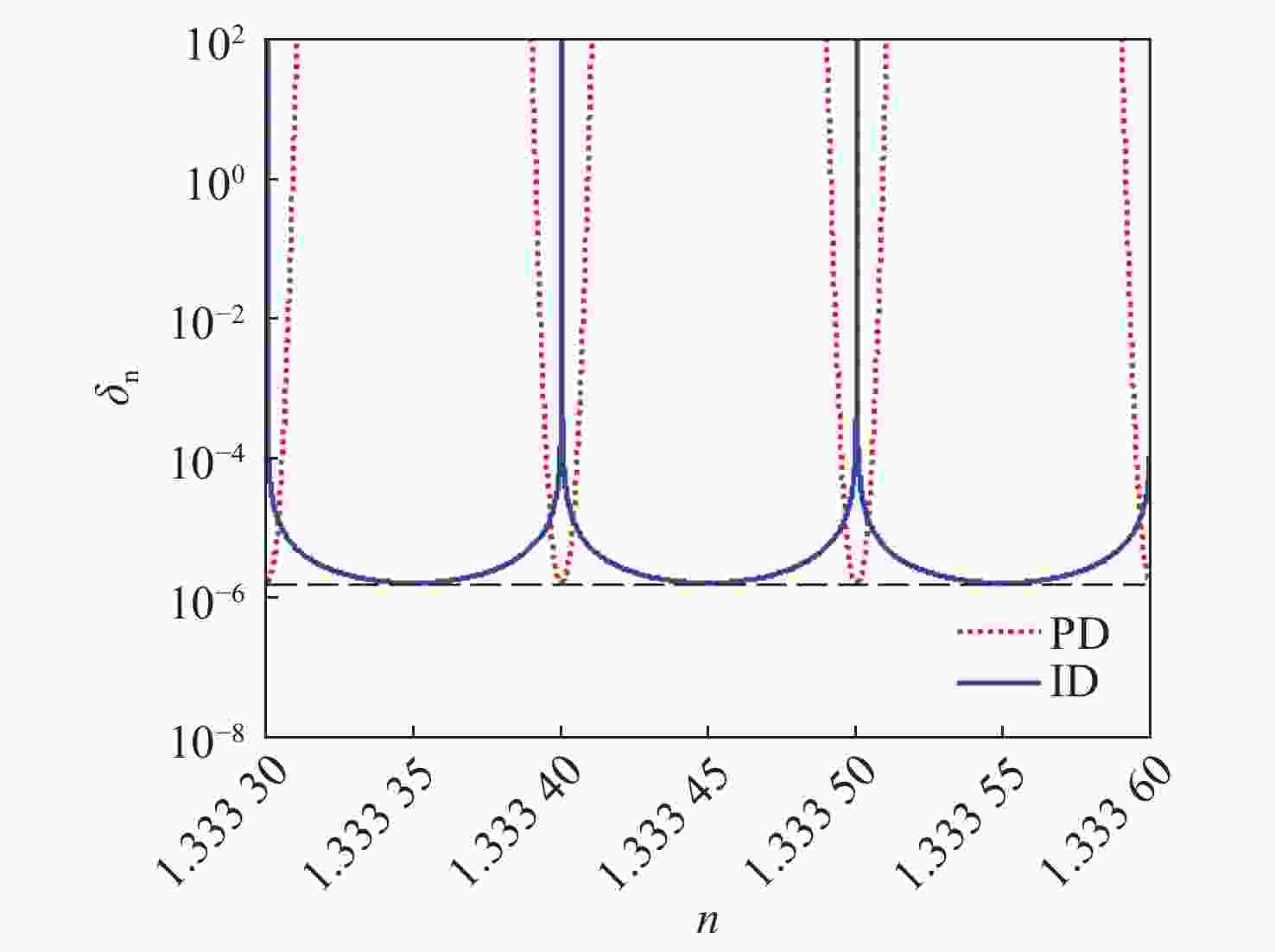
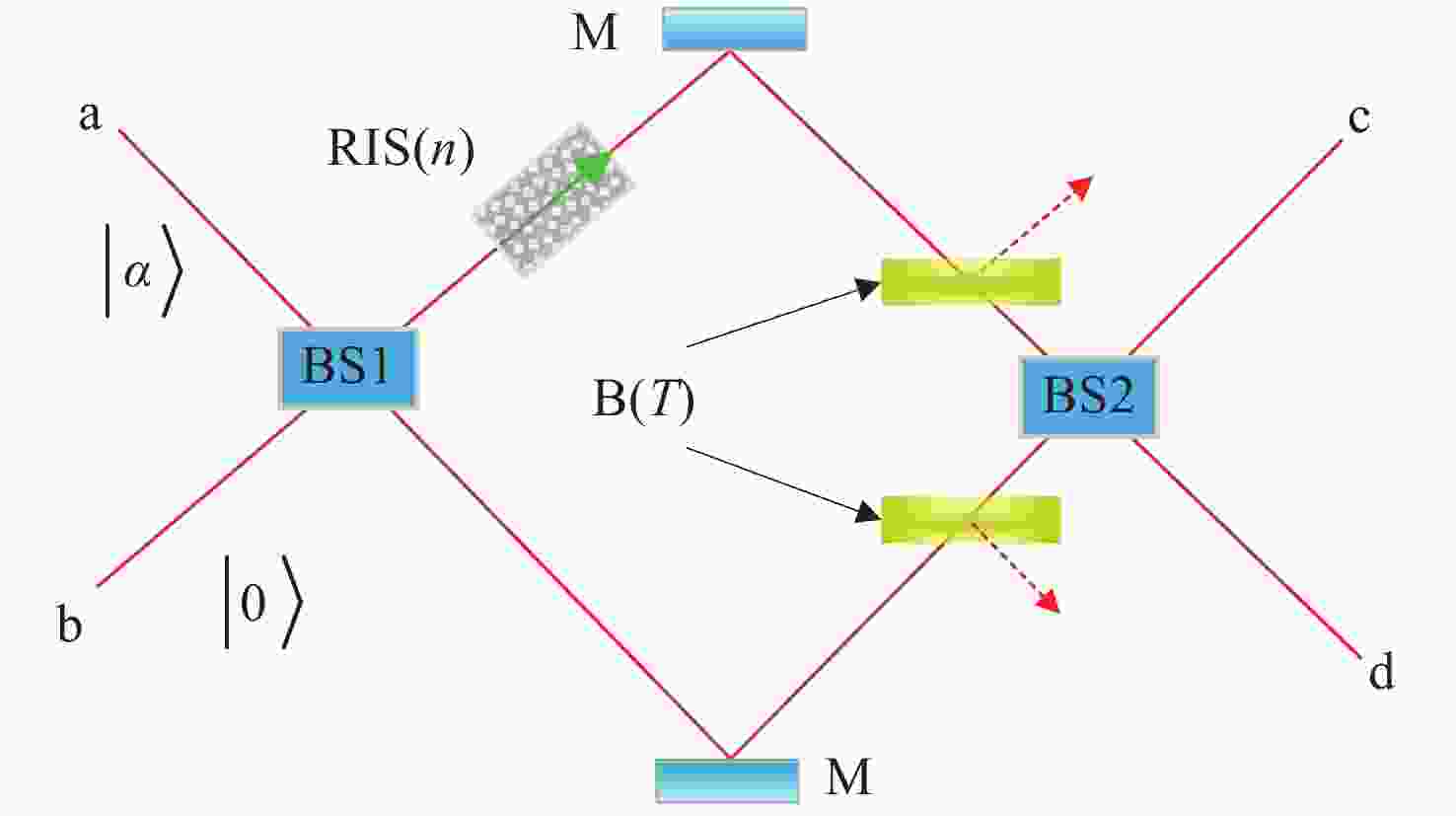
图 3奇偶探测信号和归一化强度探测信号随折射率n的变化，输入信号的平均光子数
$N = 100$ ，红色点线和黑色实线分别代表奇偶探测信号和归一化强度探测信号Figure 3.Signals of parity detection and normalized intensity detection are plotted as a function of refractive indexnfor the average photon number of
$N = 100$ . The red dotted line and black solid line represent parity detection (PD) and normalized intensity detection (ID) respectively
图 4奇偶探测和强度探测的FWHMs随着平均光子数(a)和透过率(b)的变化规律
Figure 4.FWHMs of parity and intensity detections varying with the average photon number (a) and transmittance (b)
图 5奇偶探测（红色点线）和强度探测（蓝色实线）信号灵敏度曲线，黑色虚线为两条曲线的公切线
Figure 5.Sensitivity curves of parity detection (red dotted line) and intensity detection (blue solid line), and the black dashed line represents their common tangents
图 6奇偶探测和强度探测信号最佳灵敏度随着透过率 (a) 和光子数 (b) 的变化曲线，红色点虚线表示奇偶探测，蓝色实线代表强度探测
Figure 6.Optimal sensitivity of parity detection and intensity detection signals varying with transmittance (a) and photon number (b). The red dot dashed line indicates parity detection and the blue solid line represents intensity detection
-
[1] EL-KASHEF H. Study of the refractive properties of laser dye solvents: toluene, carbon disulphide, chloroform, and benzene[J].Optical Materials, 2002, 20(2): 81-86.doi:10.1016/S0925-3467(02)00019-8 [2] 裴乃奇. 海水折射率测量系统优化和实验研究[D]. 武汉: 华中科技大学, 2017.PEI N Q. Optimization and experiment on seawater’s refractive index measurement system[D]. Wuhan: Huazhong University of Science and Technology, 2017. (in Chinese) [3] INDRASARI W, UMIATIN U, FITRIANI N. Measurement system development of refractive index, salinity and magnetic field parameters on liquid waste polluted water[J].Journal of Physics:Conference Series, 2021, 1869: 012201.doi:10.1088/1742-6596/1869/1/012201 [4] CONTEDUCA D, BARTH I, PITRUZZELLO G,et al. Dielectric nanohole array metasurface for high-resolution near-field sensing and imaging[J].Nature Communications, 2021, 12(1): 3293.doi:10.1038/s41467-021-23357-9 [5] 张静. 迈克尔逊等倾干涉法晶体折射率测量方法研究[D]. 济南: 山东大学, 2009.ZHANG J. Measurement of crystal refractive index based on Michelson interferometry[D]. Ji′nan: Shandong University, 2009. (in Chinese) [6] HU Y, LV J H, HAO Q. Refractive index measurement of glass with arbitrary shape based on Brewster’s law and a focusing probe beam[J].Sensors, 2021, 21(7): 2421.doi:10.3390/s21072421 [7] FU X L, FENG J, FAN X H,et al. Optimization design and test of a high-precision measuring device of liquid refractive index based on the method of minimum deviation angle[J].Chinese Optics, 2022, 15(4): 789-796. (in Chinese)doi:10.37188/CO.2022-0064 [8] LI G Q, CEN X, SU J,et al. Fabry-Perot cavity enhanced Prism for highly sensitive refractive index measurement of Water[J].Optik, 2021, 245: 167688.doi:10.1016/j.ijleo.2021.167688 [9] WANG W SH, XU B, ZHANG J. The principle formula error of measuring the refractive index by the method of minimum deviation angle and the method of V-prism[J].Journal of Changchun Institute of Optics and Fine Mechanics, 1995, 18(1): 5-10. (in Chinese) [10] IDRIS N, MASWATI, YUSIBANI E. The effect of the thickness of the glass plate of a hollow prism on the accuracy of measuring the refractive index of edible oil[J].Optik, 2020, 217: 164834.doi:10.1016/j.ijleo.2020.164834 [11] LIU J Q, ZHENG Y Q, YANG X M,et al. Measurement of refractive index of potassium chloride and phenolphthalein by wedge interferometry[J].The Wind of Science and Technology, 2020(21): 105. (in Chinese) [12] DU D R, LI Y, SHANG CH L,et al. Measurement of liquid refractive index by Michelson interferometer[J].Physical Experiment of College, 2019, 32(1): 43-45. (in Chinese) [13] SANJID M A, CHAUDHARY K P. Measurement of refractive index of liquids using length standards traceable to SI unit[J].MAPAN, 2016, 31(2): 89-95.doi:10.1007/s12647-015-0154-0 [14] STONE J, EGAN P, GERTY D,et al. Picometer metrology for precise measurement of refractive index, pressure, and temperature[J].NCSLI Measure, 2013, 8(4): 67-73.doi:10.1080/19315775.2013.11721666 [15] ZHANG L Y, GU J G. Discussion on relation between Interference and refractive index of Newtonian rings based on Mathematica[J].Guangxi Physics, 2021, 42(1): 28-32. (in Chinese) [16] WEI F H, ZHANG X J, TANG SH F. Design and analysis of photonic crystal fiber refractive index sensor based on surface Plasmon resonance[J].Semiconductor Optoelectronics, 2020, 41(1): 35-38,43. (in Chinese) [17] ZHANG H Y, ZHAO H H, XU X Y,et al. Measurement of water refractive index by dispersive interferometry[J].Laser&Infrared, 2020, 50(7): 781-788. (in Chinese) [18] CHOI H J, LIM H H, MOON H S,et al. Measurement of refractive index and thickness of transparent plate by dual-wavelength interference[J].Optics Express, 2010, 18(9): 9429-9434.doi:10.1364/OE.18.009429 [19] BOTO A N, KOK P, ABRAMS D S,et al. Quantum interferometric optical lithography: exploiting entanglement to beat the diffraction limit[J].Physical Review Letters, 2000, 85(13): 2733-2736.doi:10.1103/PhysRevLett.85.2733 [20] ZHANG X CH, PAN R, HAN J Y,et al. Recent progress and prospects of topological quantum material-based photodetectors[J].Chinese Optics, 2021, 14(1): 43-65. (in Chinese)doi:10.37188/CO.2020-0096 [21] BOLLINGER J J, ITANO W M, WINELAND D J,et al. Optimal frequency measurements with maximally correlated states[J].Physical Review A, 1996, 54(6): R4649-R4652.doi:10.1103/PhysRevA.54.R4649 [22] GERRY C C. Heisenberg-limit interferometry with four-wave mixers operating in a nonlinear regime[J].Physical Review A, 2000, 61(4): 043811.doi:10.1103/PhysRevA.61.043811 [23] DISTANTE E, JEŽEK M, ANDERSEN U L. Deterministic superresolution with coherent states at the shot noise limit[J].Physical Review Letters, 2013, 111(3): 033603.doi:10.1103/PhysRevLett.111.033603 [24] ANISIMOV P M, RATERMAN G M, CHIRUVELLI A,et al. Quantum metrology with two-mode squeezed vacuum: parity detection beats the Heisenberg limit[J].Physical Review Letters, 2010, 104(10): 103602.doi:10.1103/PhysRevLett.104.103602 -
下载:
点击查看大图
计量
- 文章访问数:408
- HTML全文浏览量:175
- PDF下载量:254
- 被引次数:0
