-
摘要:
周期光学系统，如光子晶体和光学超材料，可以在亚波长尺度形成高密度的电磁场能量局域，并获得极小的模式体积，在光操控领域具有巨大的应用潜力。近年来，研究人员在周期光学系统中发现一种光与物质的强相互作用，其被称为连续域束缚态。它是一类频率位于辐射连续域内但被完全局域的特殊电磁本征态，具有诸多有趣的物理特性和丰富的应用场景。本文系统性综述了周期光学系统中连续域束缚态的分类及其理论体系，并总结了其基本物理特性和最新应用发展。周期光学系统中的连续域束缚态正在为集成光学、信息光学、生物光学、拓扑光学以及非线性光学等领域注入新的发展动力。
Abstract:Periodic optical systems, such as photonic crystals and optical metamaterials, can localize high-density electromagnetic field energy at subwavelength scales and obtain extremely small mode volumes, so they have great application potential in the field of light manipulation. In recent years, a strong interaction between light and matter in periodic optical systems has been discovered, which is called Bound States in Continuum (BIC). Optics BICs are special electromagnetic eigenstates whose frequencies lie in the radiation continuum but are completely localized, and have shown interesting physics and rich application scenarios. This paper systematically reviews the classification and theory of BICs in periodic optical systems, and summarizes their basic physical properties and the latest application development. BICs in periodic optical systems are injecting new impetus into the fields of integrated optics, information optics, bio-optics, topological optics, and nonlinear optics.
-
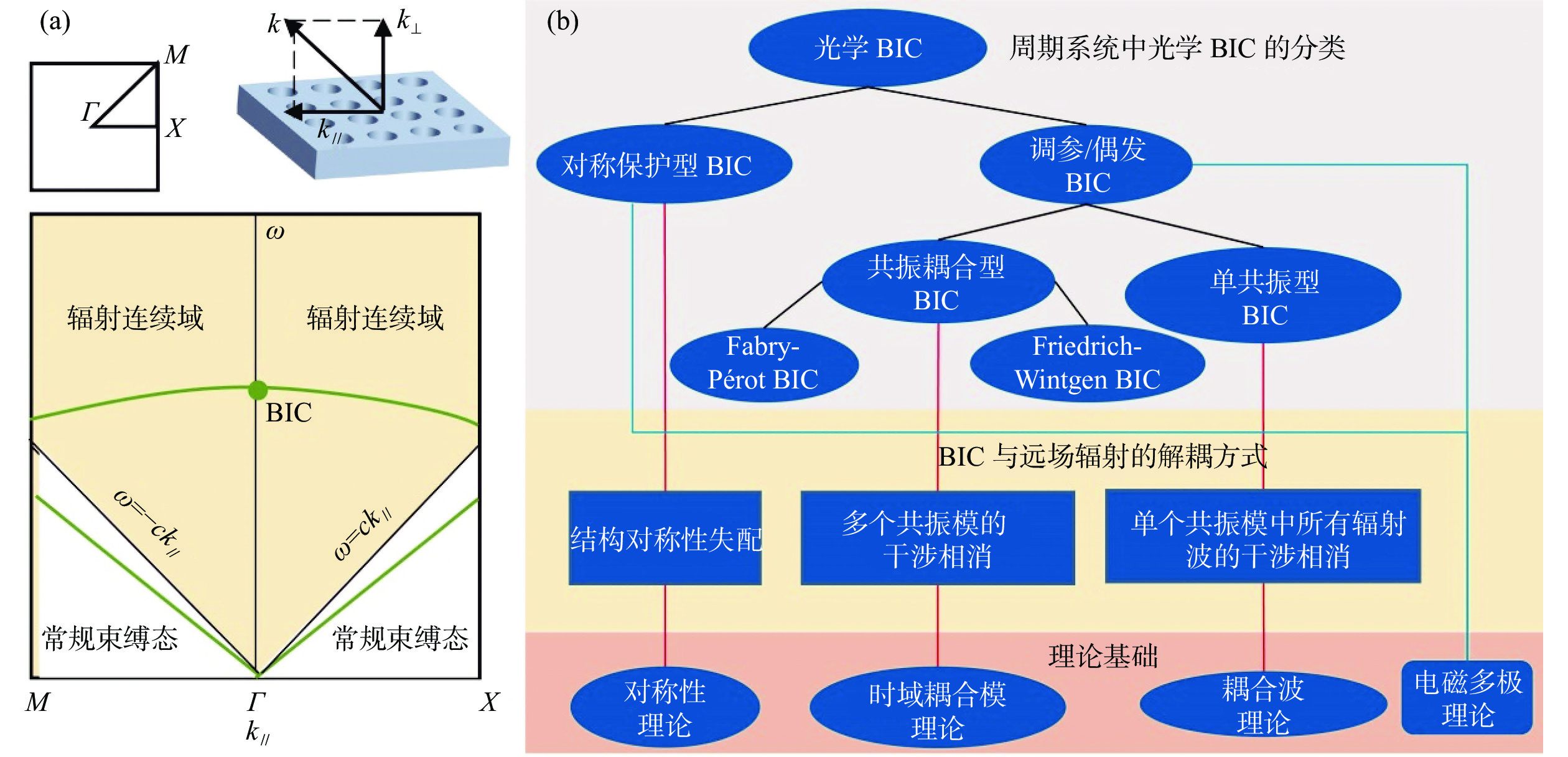
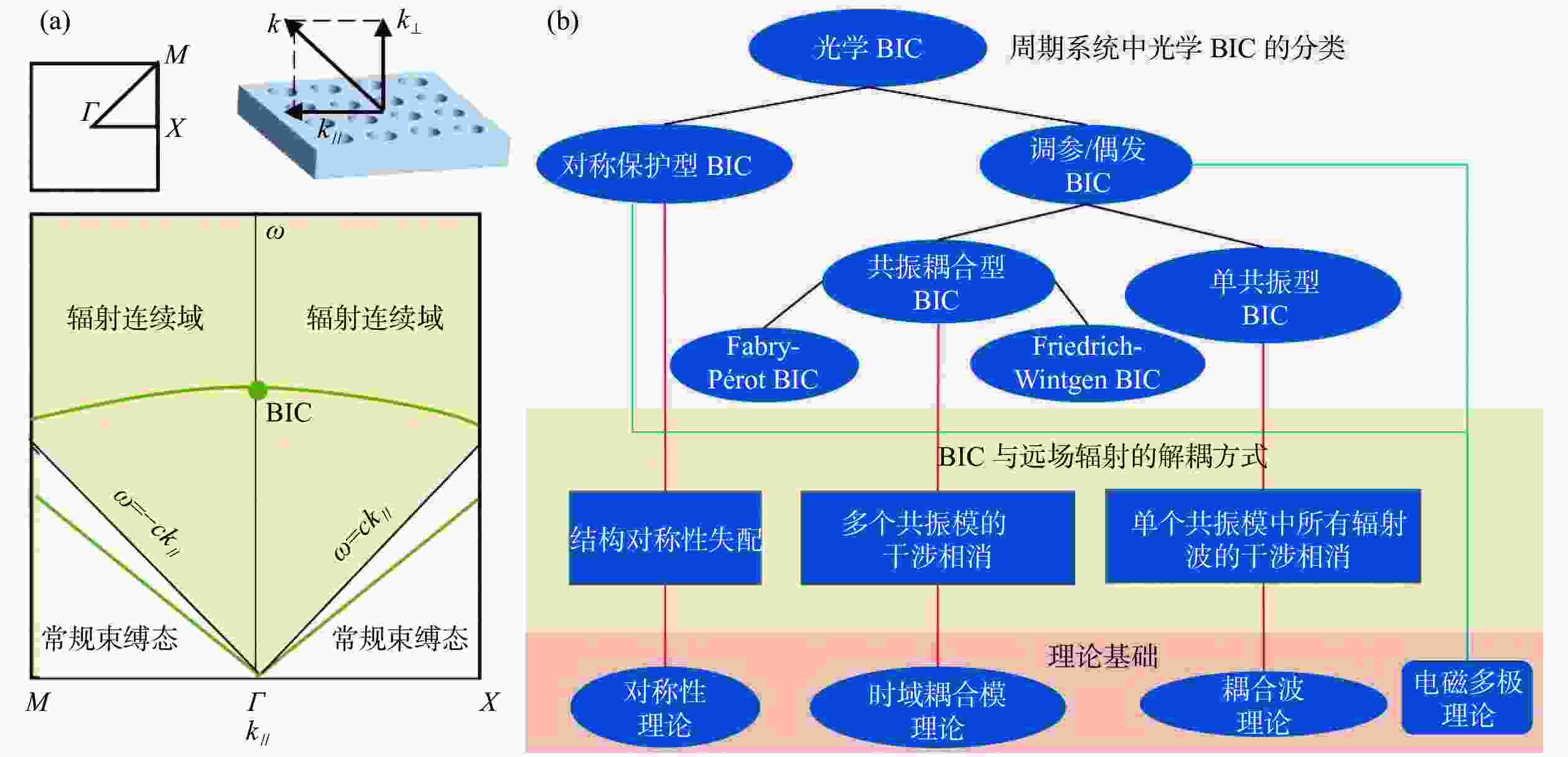
图 1 BIC的概念与分类。（a）周期光学系统的带结构中辐射共振模、BIC与普通束缚态的带位置示意图，此处以对称保护型BIC为例，它位于波矢空间的高对称点（Γ点）；（b）周期系统中光学BIC分类、与远场去偶方式及其基础理论图表
Figure 1. The concept and classification of BICs. (a) Schematic diagram for the positions of radiation resonance modes, BICs and ordinary bound states in the band structure of periodic optical systems, the symmetry-protected BIC is taken as an example, which is located at the high symmetry point (Γ point) of the wave vector space; (b) the diagram for the classification, far-field decoupling approaches and fundamentals of optics BICs in periodic systems
图 2 对称保护型BIC。（a）圆孔光子晶体板约束频率低于衍射限下的偶对称电磁模，而辐射奇对称电磁模；（b）常见的因C2对称性破坏而支持准BIC的结构；(c)品质因子随着结构不对称程度增强而降低，具有Q=Q0 α−2的关系
Figure 2. Symmetry-protected BICs. (a) Even-symmetric modes when the constraint frequency of the circular-hole photonic crystal plate is below the diffraction limit, while odd-symmetric modes radiate out the circular-hole photonic crystal plate; (b) the common structures that support quasi-BIC due to C2 symmetry is broken; (c) the quality factor decreases with increasing structural asymmetry, showing the relationship Q=Q0 α−2
图 3 共振耦合型BIC。（a）两个完全相同的高反射光子晶体板支持的Fabry–Pérot BIC，（b）其的共振机制示意图：调节两个平板共振器距离d形成驻波；（c）单独一个周期结构器件中两个模式耦合示意图，（d）两个模式耦合成一个高Q模的辐射谱；（e）频率调谐谱，调节结构参数，两个本征频率移动并交叉，在交叉点附近，一个频率的共振阻尼将完全消失形成Friedrich–Wintgen BIC，（f）在透射光谱上该点表现为平滑的谱线。[96] © 2020 Optical Society of America
Figure 3. Resonance-coupled BICs. (a) Fabry–Pérot BIC supported by two identical highly reflective photonic crystal plates, and its mechanism is shown in (b): adjust the distance d of the two plate resonators to form a standing wave; (c) schematic diagram of the coupling of two modes in a periodic structure device, (d) the radiation spectrum coupled by the two modes with high-Q mode; (e) the frequency tuning spectrum, adjusting the structural parameters, the two eigenfrequencies move and cross, and the resonance damping of one frequency will disappear completely forming the Friedrich–Wintgen BIC near the crossover point, (f) the BIC point appears as a smooth line on the transmission spectrum.[96] © 2020 Optical Society of America
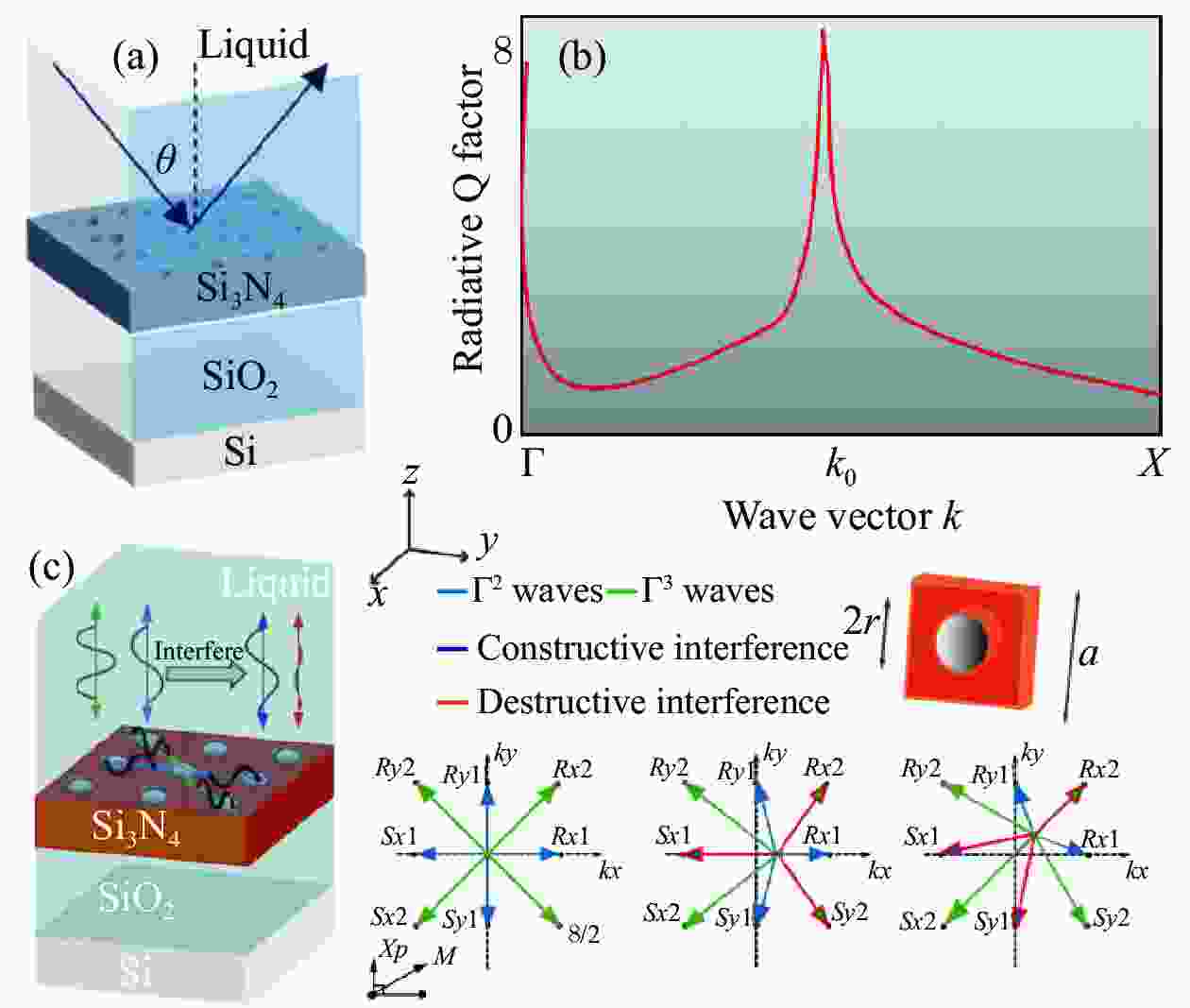
图 4 单共振型BIC。（a）调节入射波矢可以再次进入BIC，其Q因子变化如（b）；（c）耦合波理论对单共振型BIC来源解释示意图，认为其来源于耦合到开放通道中的所有波干涉相消[99]
Figure 4. Single-resonance BICs. (a) Adjust the incident wave vector to enter the BIC again, and its Q factor changes as shown in (b); (c) schematic diagram of the coupled-wave theory explaining the source of the single-resonance BIC, which is considered to be derived from the destructive interference of all waves coupled into the open channel[99]
图 5 BIC的电磁多极理论。（a）电磁多极子构造及其辐射图像[111]；（b）周期结构中多极子辐射示意图，以及（c）对称保护型BIC和偶发BIC的多极子作用机制[107]
Figure 5. Electromagnetic multipole theory of BICs. (a) Electromagnetic multipole structures and its radiation images[111]; (b) schematic diagram of multipole radiation in periodic structure, and (c) multipole interaction mechanism of symmetry-protected BIC and accidental BIC[107]
图 6 BIC与准BIC在动量空间中的辐射偏振特性[116]。（a）以对称保护型BIC为例的动量空间中的辐射偏振态；（b）打破C2对称性后，动量空间辐射偏振态变化示意图；（c）准BIC的动量空间辐射偏振态可覆盖整个庞加莱球面
Figure 6. Radiation polarization characteristics of BICs and quasi-BICs in momentum space [116]. (a) The radiation polarization states in the momentum space with the symmetry-protected BIC as an example; (b) the schematic diagram for the change of the radiation polarization states in momentum space after breaking the C2 symmetry; (c) radiation polarization states in momentum space of the quasi-BIC can cover the entire Poincaré sphere
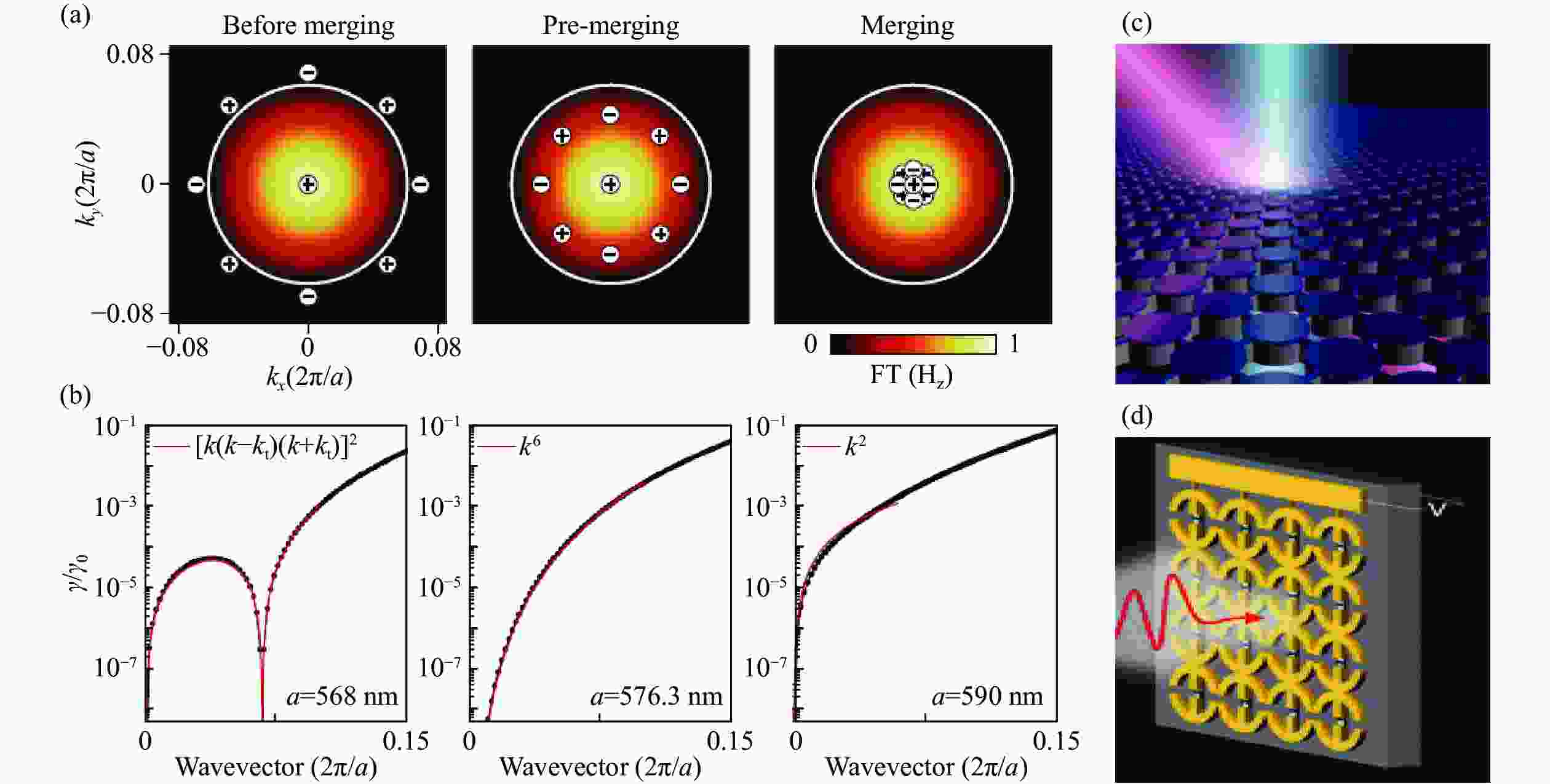
图 7 高品质因子准BIC与动态BIC构建。（a）圆孔光子晶体平板支持动量空间中多个BIC，调节周期尺寸，所有偏心BIC逐渐合并成一个BIC；（b）合并前后准BIC的Q因子变化图，合并的准BIC的Q因子始终大于孤立准BIC的Q因子[119]；（c）基于光掺杂圆柱硅的动态BIC结构和功能示意图[123] © 2019 Optical Society of America；（d）图形化石墨烯-金属超表面器件图，该器件通过调节石墨烯费米能级实现BIC与准BIC动态切换
Figure 7. Construction for quasi-BICs with high Q factor and dynamic BICs. (a) Photonic crystal slab supporting several BICs, adjusting the period size, all BICs are gradually merged into one BIC; (b) the Q factor change diagram of the quasi-BIC before and after the merger, where the Q factor of the merged quasi-BIC is always greater than that of isolated quasi-BIC[119]; (c) schematic diagram for the structure and function of dynamic BICs based on photo-doped rectangular and cylindrical silicon[123] © 2019 Optical Society of America; (d) a patterned graphene-metal metasurface device by tuning the graphene Fermi-energy level realizes dynamic switching between BIC and quasi-BIC
图 8 周期光学系统中BIC的前沿应用
Figure 8. Advanced applications of BICs in periodic optical systems
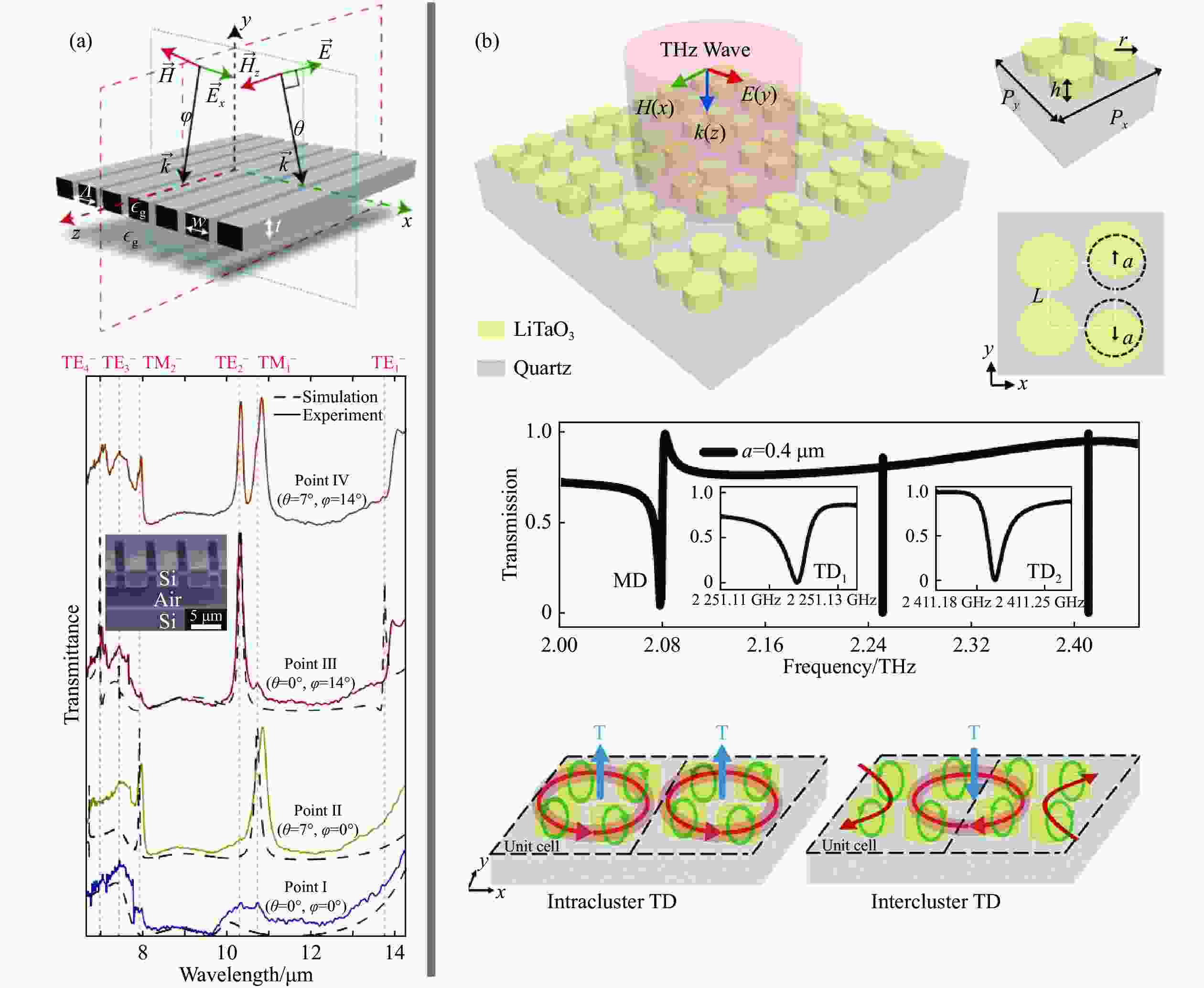
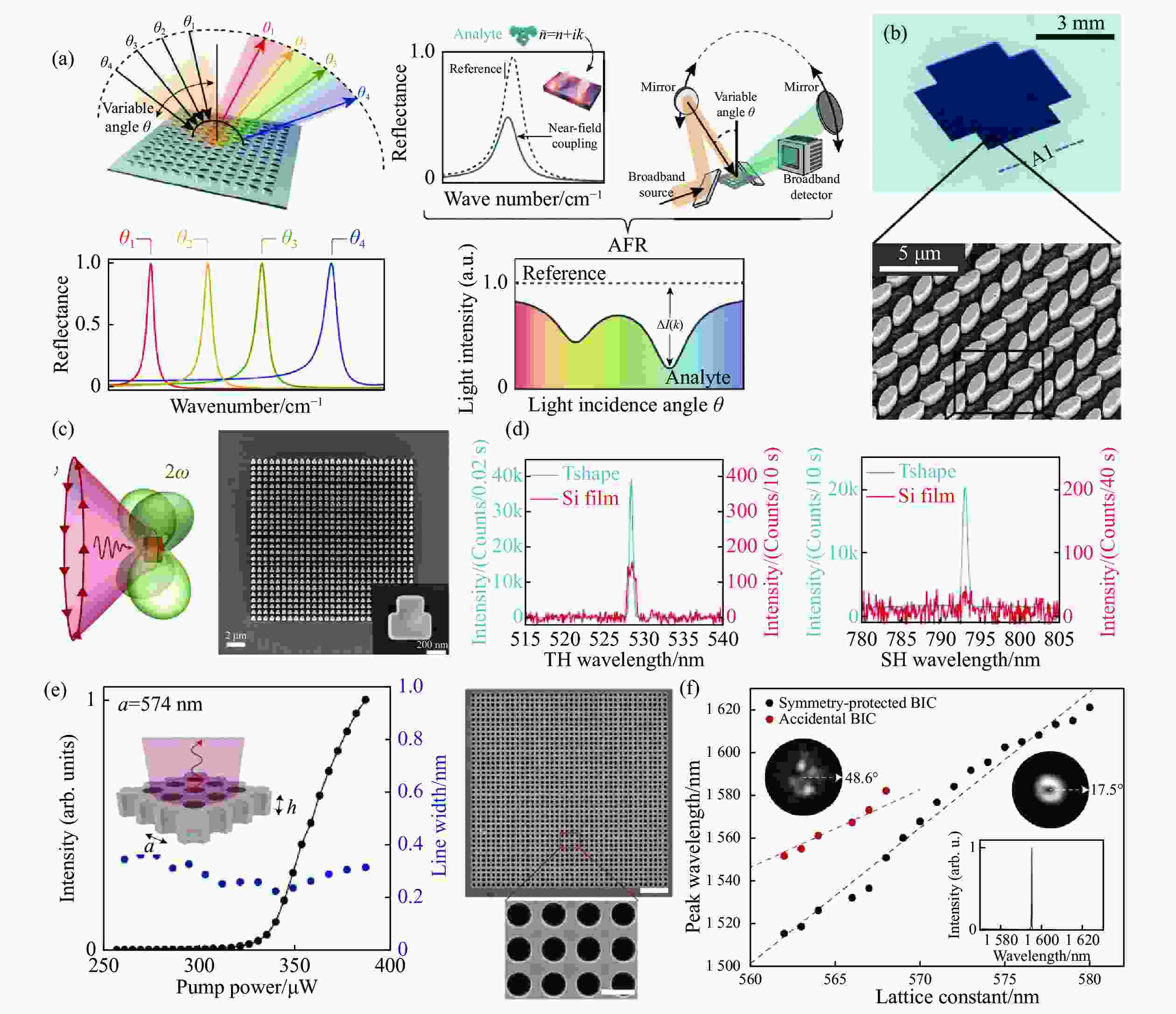
图 9 BIC在窄带滤波与传感方面的应用。（a）支持准BIC的光子晶体光栅，准BIC在低透射率背景下出现窄透射峰，实现空间窄带滤波功能[71]；（b）基于全介质四聚体的准BIC高灵敏传感器平台[68]
Figure 9. Applications of BICs in narrowband filtering and sensing. (a) Photonic crystal grating supporting quasi-BIC, quasi-BIC has narrow transmission peaks in the low background transmittance, and realizes the function of spatial narrow-band filtering[71]; (b) high-sensitive molecular sensor based on all dielectric tetramer supporting quasi-BIC[68]
图 10 （a~b）BIC分子光谱编码等像基应用[65]；（c~d）展示BIC在非线性领域的应用，这里（c）为用于产生倍频光的T字准BIC器件，（d）为三次谐波和二次谐波强度与普通器件的效果对比[130]；（e）产生微 的准BIC超表面的泵浦功率与 输出功率的关系，及其（f）周期尺寸和 波长对应关系[119]
Figure 10. (a~b) Applications of BICs based on molecular spectral coding [65]. (c~d) The non-linear applications of BICs, where (c) shows a T-shaped quasi-BIC device for generating frequency doubling light, and (d) show the comparison of the third harmonic and second harmonic intensities with those of ordinary devices [130]. (e) The relationship between pump power and light emission intensity, for quasi-BIC metasurface used to generate micro laser, and (f) the relationship between period size and laser and output power[119]
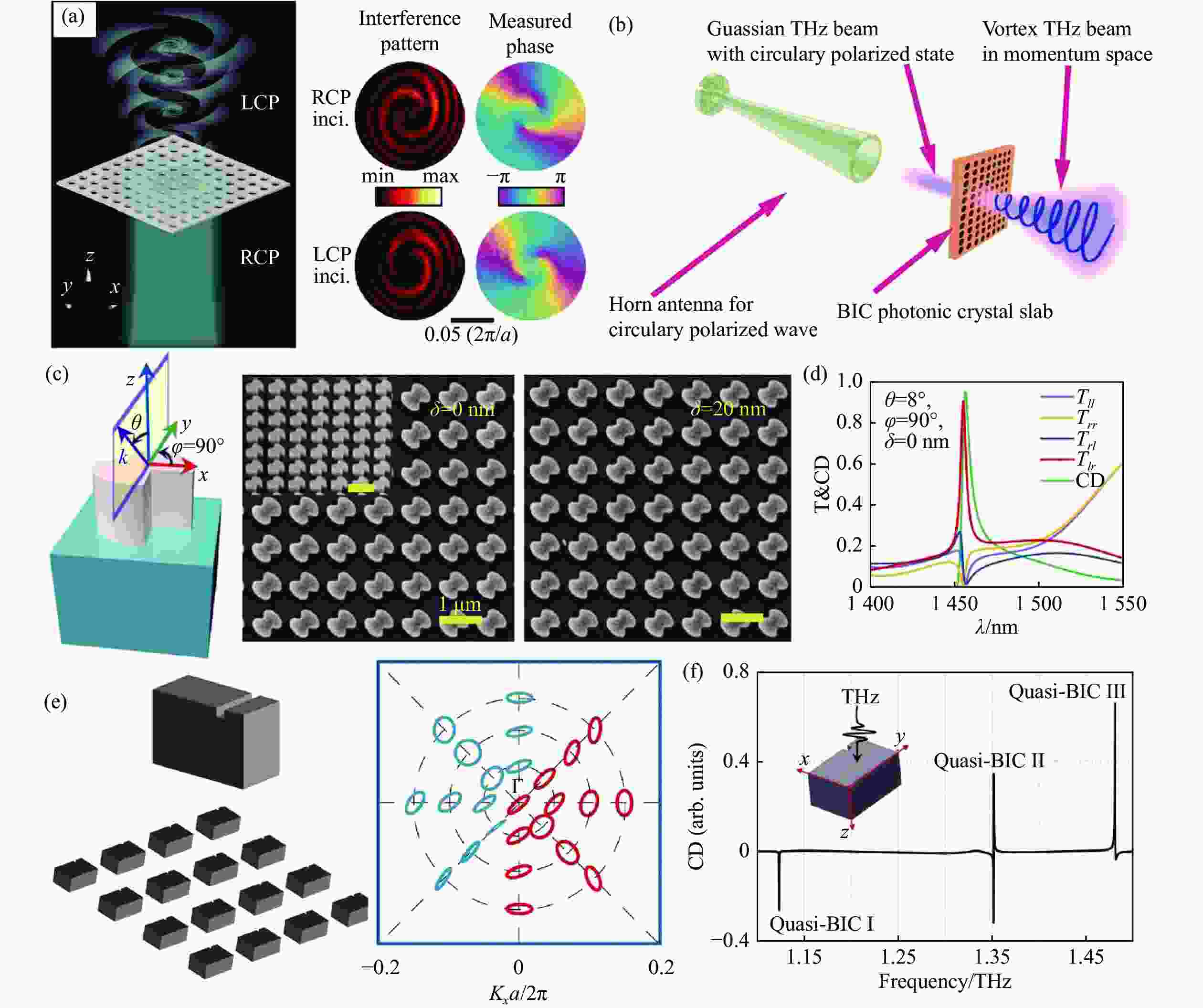
图 11 （a）基于BIC光子晶体板的动量空间涡旋束产生示意图，动量空间辐射偏振分布（左）和圆偏振入射时测试的电场相位和强度分布（右）[136]；（b）本课题组提出的将BIC光子晶体板与太赫兹圆极化天线结合以制作涡旋拓扑荷可调的太赫兹涡旋天线的构想示意图。（c~f）BIC在不对称传输领域的应用。（c）支持手性准BIC的平坦结构器件图，及其（d）圆偏振透射谱和圆二色性谱[137]；（e）基于面内C2对称性和面内镜像对称同步破坏的手性准BIC器件示意图（左）与动量空间偏振分布（右），及其（f）包含多个手性准BIC的圆二色性谱[101]
Figure 11. (a) Schematic diagram for vortex beam generation in momentum space based on photonic crystal plate supporting BIC, the radiation polarization distribution in momentum space (left) and electric field phase and intensity distribution under circularly polarized incidence (right)[78-79]; (b) schematic diagram of a concept proposed by our group by combining BIC photonic crystal slab with THz circularly polarized antenna to make THz vortex antenna with adjustable vortex topological charge. (c~f) Applications of BICs in the field of asymmetric transmission: (c) schematic diagram of the planar structure device supporting the chiral quasi-BIC, and its (d) circularly polarized transmission spectrum and circular dichroism spectrum[137]; (e) schematic diagram for a metasurface supporting the chiral quasi-BIC, with in-plane C2 symmetry and in-plane mirror symmetry breaking simultaneously (left), and its polarization distribution in momentum space (right), and (f) its circular dichroism spectrum containing multiple chiral quasi-BICs[101]
-
[1] VON NEUMANN J, WIGNER E P. Uber merkwürdige diskrete eigenwerte[J]. Physikalische Zeitschrift, 1929, 30: 465-467. [2] VOO K K. Trapped electromagnetic modes in forked transmission lines[J]. Wave Motion, 2008, 45(6): 795-803. doi: 10.1016/j.wavemoti.2008.02.001 [3] CALLAN M, LINTON C M, EVANS D V. Trapped modes in two-dimensional waveguides[J]. Journal of Fluid Mechanics, 1991, 229: 51-64. doi: 10.1017/S0022112091002938 [4] COBELLI P J, PAGNEUX V, MAUREL A, et al. Experimental observation of trapped modes in a water wave channel[J]. Europhysics Letters, 2009, 88(2): 20006. doi: 10.1209/0295-5075/88/20006 [5] COBELLI P J, PAGNEUX V, MAUREL A, et al. Experimental study on water-wave trapped modes[J]. Journal of Fluid Mechanics, 2011, 666: 445-476. doi: 10.1017/S0022112010004222 [6] LINTON C M, MCIVER P. Embedded trapped modes in water waves and acoustics[J]. Wave Motion, 2007, 45(1-2): 16-29. doi: 10.1016/j.wavemoti.2007.04.009 [7] HEIN S, KOCH W, NANNEN L. Trapped modes and Fano resonances in two-dimensional acoustical duct–cavity systems[J]. Journal of Fluid Mechanics, 2012, 692: 257-287. doi: 10.1017/jfm.2011.509 [8] LYAPINA A A, MAKSIMOV D N, PILIPCHUK A S, et al. Bound states in the continuum in open acoustic resonators[J]. Journal of Fluid Mechanics, 2015, 780: 370-387. doi: 10.1017/jfm.2015.480 [9] ALSHITS V I, DARINSKII A N, SHUVALOV A L. Elastic waves in infinite and semi-infinite anisotropic media[J]. Physica Scripta, 1992, 1992(T44): 85-93. [10] EVERY A G. Guided elastic waves at a periodic array of thin coplanar cavities in a solid[J]. Physical Review B, 2008, 78(17): 174104. doi: 10.1103/PhysRevB.78.174104 [11] BULGAKOV E N, SADREEV A F. Bound states in the continuum in photonic waveguides inspired by defects[J]. Physical Review B, 2008, 78(7): 075105. doi: 10.1103/PhysRevB.78.075105 [12] MARINICA D C, BORISOV A G, SHABANOV S V. Bound States in the continuum in photonics[J]. Physical Review Letters, 2008, 100(18): 183902. doi: 10.1103/PhysRevLett.100.183902 [13] LONGHI S. Optical analog of population trapping in the continuum: classical and quantum interference effects[J]. Physical Review A, 2009, 79(2): 023811. doi: 10.1103/PhysRevA.79.023811 [14] PLOTNIK Y, PELEG O, DREISOW F, et al. Experimental observation of optical bound states in the continuum[J]. Physical Review Letters, 2011, 107(18): 183901. doi: 10.1103/PhysRevLett.107.183901 [15] LEE J, ZHEN B, CHUA S L, et al. Observation and differentiation of unique high-Q optical resonances near zero wave vector in macroscopic photonic crystal slabs[J]. Physical Review Letters, 2012, 109(6): 067401. doi: 10.1103/PhysRevLett.109.067401 [16] WEIMANN S, XU Y, KEIL R, et al. Compact surface Fano states embedded in the continuum of waveguide arrays[J]. Physical Review Letters, 2013, 111(24): 240403. doi: 10.1103/PhysRevLett.111.240403 [17] BULGAKOV E N, SADREEV A F. Robust bound state in the continuum in a nonlinear microcavity embedded in a photonic crystal waveguide[J]. Optics Letters, 2014, 39(17): 5212-5215. doi: 10.1364/OL.39.005212 [18] YOON J W, SONG S H, MAGNUSSON R. Critical field enhancement of asymptotic optical bound states in the continuum[J]. Scientific Reports, 2015, 5: 18301. doi: 10.1038/srep18301 [19] ZHANG M D, ZHANG X D. Ultrasensitive optical absorption in graphene based on bound states in the continuum[J]. Scientific Reports, 2015, 5: 8266. doi: 10.1038/srep08266 [20] BULGAKOV E N, SADREEV A F. Transfer of spin angular momentum of an incident wave into orbital angular momentum of the bound states in the continuum in an array of dielectric spheres[J]. Physical Review A, 2016, 94(3): 033856. doi: 10.1103/PhysRevA.94.033856 [21] LI L SH, YIN H CH. Bound States in the Continuum in double layer structures[J]. Scientific Reports, 2016, 6: 26988. doi: 10.1038/srep26988 [22] NI L F, WANG ZH X, PENG CH, et al. Tunable optical bound states in the continuum beyond in-plane symmetry protection[J]. Physical Review B, 2016, 94(24): 245148. doi: 10.1103/PhysRevB.94.245148 [23] GOMIS-BRESCO J, ARTIGAS D, TORNER L. Anisotropy-induced photonic bound states in the continuum[J]. Nature Photonics, 2017, 11(4): 232-236. doi: 10.1038/nphoton.2017.31 [24] SADREEV A F, PILIPCHUK A S, LYAPINA A A. Tuning of Fano resonances by rotation of continuum: wave faucet[J]. Europhysics Letters, 2017, 117(5): 50011. doi: 10.1209/0295-5075/117/50011 [25] SADRIEVA Z F, SINEV I S, KOSHELEV K L, et al. Transition from optical bound states in the continuum to leaky resonances: role of substrate and roughness[J]. ACS Photonics, 2017, 4(4): 723-727. doi: 10.1021/acsphotonics.6b00860 [26] BULGAKOV E N, MAKSIMOV D N, SEMINA P N, et al. Propagating bound states in the continuum in dielectric gratings[J]. Journal of the Optical Society of America B, 2018, 35(6): 1218-1222. doi: 10.1364/JOSAB.35.001218 [27] KOSHELEV K L, SYCHEV S K, SADRIEVA Z F, et al. Strong coupling between excitons in transition metal dichalcogenides and optical bound states in the continuum[J]. Physical Review B, 2018, 98(16): 161113(R). doi: 10.1103/PhysRevB.98.161113 [28] LIU M K, CHOI D Y. Extreme Huygens' metasurfaces based on quasi-bound states in the continuum[J]. Nano Letters, 2018, 18(12): 8062-8069. doi: 10.1021/acs.nanolett.8b04774 [29] MINKOV M, WILLIAMSON I A D, XIAO M, et al. Zero-index bound states in the continuum[J]. Physical Review Letters, 2018, 121(26): 263901. doi: 10.1103/PhysRevLett.121.263901 [30] LI SH Y, ZHOU CH B, LIU T T, et al. Symmetry-protected bound states in the continuum supported by all-dielectric metasurfaces[J]. Physical Review A, 2019, 100(6): 063803. doi: 10.1103/PhysRevA.100.063803 [31] YU Z J, SUN X K. Acousto-optic modulation of photonic bound state in the continuum[J]. Light:Science &Applications, 2020, 9: 1. [32] YU Z J, TONG Y Y, TSANG H K, et al. High-dimensional communication on etchless lithium niobate platform with photonic bound states in the continuum[J]. Nature Communications, 2020, 11(1): 2602. doi: 10.1038/s41467-020-15358-x [33] LI ZH, LIU W W, GENG G ZH, et al. Multiplexed nondiffracting nonlinear metasurfaces[J]. Advanced Functional Materials, 2020, 30(23): 1910744. doi: 10.1002/adfm.201910744 [34] LI J, LI J T, ZHENG CH L, et al. Broadband and tunable terahertz absorption via photogenerated carriers in undoped silicon[J]. Science China Physics,Mechanics &Astronomy, 2021, 65(1): 214211. [35] LI J, ZHENG CH L, WANG G C, et al. Circular dichroism-like response of terahertz wave caused by phase manipulation via all-silicon metasurface[J]. Photonics Research, 2021, 9(4): 567-573. doi: 10.1364/PRJ.415547 [36] YUE ZH, LIU J Y, LI J T, et al. Multifunctional terahertz metasurfaces for polarization transformation and wavefront manipulation[J]. Nanoscale, 2021, 13(34): 14490-14496. doi: 10.1039/D1NR03388C [37] 柴若衡, 刘文玮, 程化, 等. 人工光学微纳结构中的连续体束缚态: 原理、发展及应用[J]. 光学学报,2021,41(1):0123001. doi: 10.3788/AOS202141.0123001CHAI R H, LIU W W, CHENG H, et al. Bound states of continuum in optical artificial micro-nanostructures: fundamentals, developments and applications[J]. Acta Optica Sinica, 2021, 41(1): 0123001. (in Chinese) doi: 10.3788/AOS202141.0123001 [38] LI J T, WANG G C, YUE ZH, et al. Dynamic phase assembled terahertz metalens for reversible conversion between linear polarization and arbitrary circular polarization[J]. Opto-Electronic Advances, 2022, 5(1): 210062. doi: 10.29026/oea.2022.210062 [39] LI J T, YUE ZH, LI J, et al. . Wavefront-controllable all-silicon terahertz meta-polarizer[J]. Science China Materials, 2022,doi: 10.1007/s40843-022-2126-0. [40] LI J T, YUE ZH, LI J, et al. . Diverse terahertz wavefront manipulations empowered by the spatially interleaved metasurfaces[J]. Science China Information Sciences, 2023,doi: 10.1007/s11432-022-3499-4. [41] YUE ZH, LI J T, LI J, et al. Terahertz metasurface zone plates with arbitrary polarizations to a fixed polarization conversion[J]. Opto-Electronic Science, 2022, 1(3): 210014. doi: 10.29026/oes.2022.210014 [42] YUE ZH, LI J T, LIU J Y, et al. Versatile polarization conversion and wavefront shaping based on fully phase‐modulated metasurface with complex amplitude modulation[J]. Advanced Optical Materials, 2022, 10(16): 2200733. doi: 10.1002/adom.202200733 [43] YUE ZH, LIU J Y, LI J T, et al. Vector beam generation based on spin-decoupling metasurface zone plate[J]. Applied Physics Letters, 2022, 120(19): 191704. doi: 10.1063/5.0093708 [44] ZHENG CH L, LI J, LIU J Y, et al. Creating longitudinally varying vector vortex beams with an all‐dielectric metasurface[J]. Laser &Photonics Reviews, 2022, 16(10): 2200236. [45] ZHENG CH L, LI J, YUE ZH, et al. All‐dielectric trifunctional metasurface capable of independent amplitude and phase modulation[J]. Laser &Photonics Reviews, 2022, 16(7): 2200051. [46] KUPRIIANOV A S, XU Y, SAYANSKIY A, et al. Metasurface engineering through bound states in the continuum[J]. Physical Review Applied, 2019, 12(1): 014024. doi: 10.1103/PhysRevApplied.12.014024 [47] ROMANO S, ZITO G, LARA YÉPEZ S N, et al. Tuning the exponential sensitivity of a bound-state-in-continuum optical sensor[J]. Optics Express, 2019, 27(13): 18776-18786. doi: 10.1364/OE.27.018776 [48] ABUJETAS D R, BARREDA Á, MORENO F, et al. High‐Q transparency band in all‐dielectric metasurfaces induced by a quasi bound state in the continuum[J]. Laser &Photonics Reviews, 2021, 15(1): 2000263. [49] MURAI S, ABUJETAS D R, CASTELLANOS G W, et al. Bound states in the continuum in the visible emerging from out-of-plane magnetic dipoles[J]. ACS Photonics, 2020, 7(8): 2204-2210. doi: 10.1021/acsphotonics.0c00723 [50] OVERVIG A C, MALEK S C, CARTER M J, et al. Selection rules for quasibound states in the continuum[J]. Physical Review B, 2020, 102(3): 035434. doi: 10.1103/PhysRevB.102.035434 [51] WANG X, DUAN J Y, CHEN W Y, et al. Controlling light absorption of graphene at critical coupling through magnetic dipole quasi-bound states in the continuum resonance[J]. Physical Review B, 2020, 102(15): 155432. doi: 10.1103/PhysRevB.102.155432 [52] XIAO SH Y, LIU T T, WANG X, et al. Tailoring the absorption bandwidth of graphene at critical coupling[J]. Physical Review B, 2020, 102(8): 085410. doi: 10.1103/PhysRevB.102.085410 [53] VAN HOOF N J J, ABUJETAS D R, TER HUURNE S E T, et al. Unveiling the symmetry protection of bound states in the continuum with terahertz near-field imaging[J]. ACS Photonics, 2021, 8(10): 3010-3016. doi: 10.1021/acsphotonics.1c00937 [54] ABUJETAS D R, VAN HOOF N, TER HUURNE S, et al. Spectral and temporal evidence of robust photonic bound states in the continuum on terahertz metasurfaces[J]. Optica, 2019, 6(8): 996-1001. doi: 10.1364/OPTICA.6.000996 [55] BOGDANOV A A, KOSHELEV K L, KAPITANOVA P V, et al. Bound states in the continuum and Fano resonances in the strong mode coupling regime[J]. Advanced Photonics, 2019, 1(1): 016001. [56] CONG L Q, SINGH R. Symmetry‐protected dual bound states in the continuum in metamaterials[J]. Advanced Optical Materials, 2019, 7(13): 1900383. [57] KYAW C, YAHIAOUI R, BURROW J A, et al. Polarization-selective modulation of supercavity resonances originating from bound states in the continuum[J]. Communications Physics, 2020, 3(1): 212. doi: 10.1038/s42005-020-00453-8 [58] LIANG Y, KOSHELEV K, ZHANG F CH, et al. Bound states in the continuum in anisotropic plasmonic metasurfaces[J]. Nano Letters, 2020, 20(9): 6351-6356. doi: 10.1021/acs.nanolett.0c01752 [59] XIANG J, XU Y, CHEN J D, et al. Tailoring the spatial localization of bound state in the continuum in plasmonic-dielectric hybrid system[J]. Nanophotonics, 2020, 9(1): 133-142. doi: 10.1515/nanoph-2019-0341 [60] NIU J Q, ZHAI Y Q, HAN Q Q, et al. Resonance-trapped bound states in the continuum in metallic THz metasurfaces[J]. Optics Letters, 2021, 46(2): 162-165. doi: 10.1364/OL.410791 [61] DONG ZH D, MAHFOUD Z, PANIAGUA-DOMÍNGUEZ R, et al. Nanoscale mapping of optically inaccessible bound-states-in-the-continuum[J]. Light:Science &Applications, 2022, 11(1): 20. [62] SONG Q J, HU J SH, DAI SH W, et al. Coexistence of a new type of bound state in the continuum and a lasing threshold mode induced by PT symmetry[J]. Science Advances, 2020, 6(34): eabc1160. doi: 10.1126/sciadv.abc1160 [63] ZHEN B, HSU C W, LU L, et al. Topological nature of optical bound states in the continuum[J]. Physical Review Letters, 2014, 113(25): 257401. doi: 10.1103/PhysRevLett.113.257401 [64] DOELEMAN H M, MONTICONE F, DEN HOLLANDER W, et al. Experimental observation of a polarization vortex at an optical bound state in the continuum[J]. Nature Photonics, 2018, 12(7): 397-401. doi: 10.1038/s41566-018-0177-5 [65] LEITIS A, TITTL A, LIU M K, et al. Angle-multiplexed all-dielectric metasurfaces for broadband molecular fingerprint retrieval[J]. Science Advances, 2019, 5(5): eaaw2871. doi: 10.1126/sciadv.aaw2871 [66] KOSHELEV K, BOGDANOV A, KIVSHAR Y. Meta-optics and bound states in the continuum[J]. Science Bulletin, 2019, 64(12): 836-842. doi: 10.1016/j.scib.2018.12.003 [67] KOSHELEV K, TANG Y T, LI K F, et al. Nonlinear metasurfaces governed by bound states in the continuum[J]. ACS Photonics, 2019, 6(7): 1639-1644. doi: 10.1021/acsphotonics.9b00700 [68] WANG Y L, HAN ZH H, DU Y, et al. Ultrasensitive terahertz sensing with high-Q toroidal dipole resonance governed by bound states in the continuum in all-dielectric metasurface[J]. Nanophotonics, 2021, 10(4): 1295-1307. doi: 10.1515/nanoph-2020-0582 [69] KANG M, ZHANG Z Y, WU T, et al. Coherent full polarization control based on bound states in the continuum[J]. Nature Communications, 2022, 13(1): 4536. doi: 10.1038/s41467-022-31726-1 [70] KÜHNER L, SORTINO L, BERTÉ R, et al. Radial bound states in the continuum for polarization-invariant nanophotonics[J]. Nature Communications, 2022, 13(1): 4992. doi: 10.1038/s41467-022-32697-z [71] FOLEY J M, YOUNG S M, PHILLIPS J D. Symmetry-protected mode coupling near normal incidence for narrow-band transmission filtering in a dielectric grating[J]. Physical Review B, 2014, 89(16): 165111. doi: 10.1103/PhysRevB.89.165111 [72] ROMANO S, ZITO G, TORINO S, et al. Label-free sensing of ultralow-weight molecules with all-dielectric metasurfaces supporting bound states in the continuum[J]. Photonics Research, 2018, 6(7): 726-733. doi: 10.1364/PRJ.6.000726 [73] TITTL A, LEITIS A, LIU M K, et al. Imaging-based molecular barcoding with pixelated dielectric metasurfaces[J]. Science, 2018, 360(6393): 1105-1109. doi: 10.1126/science.aas9768 [74] ZHOU Y, ZHENG H Y, KRAVCHENKO I I, et al. Flat optics for image differentiation[J]. Nature Photonics, 2020, 14(5): 316-323. doi: 10.1038/s41566-020-0591-3 [75] CARLETTI L, KOSHELEV K, DE ANGELIS C, et al. Giant nonlinear response at the nanoscale driven by bound states in the continuum[J]. Physical Review Letters, 2018, 121(3): 033903. doi: 10.1103/PhysRevLett.121.033903 [76] KODIGALA A, LEPETIT T, GU Q, et al. Lasing action from photonic bound states in continuum[J]. Nature, 2017, 541(7636): 196-199. doi: 10.1038/nature20799 [77] COLOM R, BINKOWSKI F, BETZ F, et al. Enhanced Purcell factor for nanoantennas supporting interfering resonances[J]. Physical Review Research, 2022, 4(2): 023189. doi: 10.1103/PhysRevResearch.4.023189 [78] HUANG C, ZHANG CH, XIAO SH M, et al. Ultrafast control of vortex microlasers[J]. Science, 2020, 367(6481): 1018-1021. doi: 10.1126/science.aba4597 [79] WANG B, LIU W ZH, ZHAO M X, et al. Generating optical vortex beams by momentum-space polarization vortices centred at bound states in the continuum[J]. Nature Photonics, 2020, 14(10): 623-628. doi: 10.1038/s41566-020-0658-1 [80] GORKUNOV M V, ANTONOV A A, KIVSHAR Y S. Metasurfaces with maximum chirality empowered by bound states in the continuum[J]. Physical Review Letters, 2020, 125(9): 093903. doi: 10.1103/PhysRevLett.125.093903 [81] HSU C W, ZHEN B, STONE A D, et al. Bound states in the continuum[J]. Nature Reviews Materials, 2016, 1(9): 16048. doi: 10.1038/natrevmats.2016.48 [82] FEDOTOV V A, ROSE M, PROSVIRNIN S L, et al. Sharp trapped-mode resonances in planar metamaterials with a broken structural symmetry[J]. Physical Review Letters, 2007, 99(14): 147401. doi: 10.1103/PhysRevLett.99.147401 [83] MANJAPPA M, SOLANKI A, KUMAR A, et al. Solution-processed lead iodide for ultrafast all-optical switching of terahertz photonic devices[J]. Advanced Materials, 2019, 31(32): 1901455. [84] EVLYUKHIN A B, BOZHEVOLNYI S I, PORS A, et al. Detuned electrical dipoles for plasmonic sensing[J]. Nano Letters, 2010, 10(11): 4571-4577. doi: 10.1021/nl102572q [85] ZHANG J F, MACDONALD K F, ZHELUDEV N I. Near-infrared trapped mode magnetic resonance in an all-dielectric metamaterial[J]. Optics Express, 2013, 21(22): 26721-26728. doi: 10.1364/OE.21.026721 [86] TIAN J Y, LI Q, BELOV P A, et al. High-Q all-dielectric metasurface: super and suppressed optical absorption[J]. ACS Photonics, 2020, 7(6): 1436-1443. doi: 10.1021/acsphotonics.0c00003 [87] LI J T, LI J, ZHENG CH L, et al. Spectral amplitude modulation and dynamic near-field displaying of all-silicon terahertz metasurfaces supporting bound states in the continuum[J]. Applied Physics Letters, 2021, 119(24): 241105. doi: 10.1063/5.0067937 [88] VABISHCHEVICH P P, LIU S, SINCLAIR M B, et al. Enhanced second-harmonic generation using broken symmetry III–V semiconductor fano metasurfaces[J]. ACS Photonics, 2018, 5(5): 1685-1690. doi: 10.1021/acsphotonics.7b01478 [89] FANG C ZH, YANG Q Y, YUAN Q CH, et al. High-Q resonances governed by the quasi-bound states in the continuum in all-dielectric metasurfaces[J]. Opto-Electronic Advances, 2021, 4(6): 200030. doi: 10.29026/oea.2021.200030 [90] MUHAMMAD N, CHEN Y, QIU CH W, et al. Optical bound states in continuum in MoS2-based metasurface for directional light emission[J]. Nano Letters, 2021, 21(2): 967-972. doi: 10.1021/acs.nanolett.0c03818 [91] TUZ V R, KHARDIKOV V V, KUPRIIANOV A S, et al. High-quality trapped modes in all-dielectric metamaterials[J]. Optics Express, 2018, 26(3): 2905-2916. doi: 10.1364/OE.26.002905 [92] HAN S, PITCHAPPA P, WANG W H, et al. Extended bound states in the continuum with symmetry‐Broken terahertz dielectric metasurfaces[J]. Advanced Optical Materials, 2021, 9(7): 2002001. doi: 10.1002/adom.202002001 [93] KIM K H, KIM J R. High‐Q chiroptical resonances by quasi‐bound states in the continuum in dielectric metasurfaces with simultaneously broken in‐plane inversion and mirror symmetries[J]. Advanced Optical Materials, 2021, 9(22): 2101162. doi: 10.1002/adom.202101162 [94] KOSHELEV K, LEPESHOV S, LIU M K, et al. Asymmetric metasurfaces with high-Q resonances governed by bound states in the continuum[J]. Physical Review Letters, 2018, 121(19): 193903. doi: 10.1103/PhysRevLett.121.193903 [95] SUH W, YANIK M F, SOLGAARD O, et al. Displacement-sensitive photonic crystal structures based on guided resonance in photonic crystal slabs[J]. Applied Physics Letters, 2003, 82(13): 1999-2001. doi: 10.1063/1.1563739 [96] ZHAO X G, CHEN CH X, KAJ K, et al. Terahertz investigation of bound states in the continuum of metallic metasurfaces[J]. Optica, 2020, 7(11): 1548-1554. doi: 10.1364/OPTICA.404754 [97] FRIEDRICH H, WINTGEN D. Interfering resonances and bound states in the continuum[J]. Physical Review A, 1985, 32(6): 3231-3242. doi: 10.1103/PhysRevA.32.3231 [98] HSU C W, ZHEN B, LEE J, et al. Observation of trapped light within the radiation continuum[J]. Nature, 2013, 499(7457): 188-191. doi: 10.1038/nature12289 [99] LIANG Y, PENG C, SAKAI K, et al. Three-dimensional coupled-wave model for square-lattice photonic crystal lasers with transverse electric polarization: a general approach[J]. Physical Review B, 2011, 84(19): 195119. doi: 10.1103/PhysRevB.84.195119 [100] YANG Y, PENG CH, LIANG Y, et al. Analytical perspective for bound states in the continuum in photonic crystal slabs[J]. Physical Review Letters, 2014, 113(3): 037401. doi: 10.1103/PhysRevLett.113.037401 [101] LI J T, YUE ZH, LI J, et al. Ultra-narrowband terahertz circular dichroism driven by planar metasurface supporting chiral quasi bound states in continuum[J]. Optics and Laser Technology, 2023. doi: 10.1016/j.optlastec.2023.109173 [102] FAN SH H, SUH W, JOANNOPOULOS J D. Temporal coupled-mode theory for the Fano resonance in optical resonators[J]. Journal of the Optical Society of America A, 2003, 20(3): 569-572. doi: 10.1364/JOSAA.20.000569 [103] SHU W, WANG ZH, FAN SH H. Temporal coupled-mode theory and the presence of non-orthogonal modes in lossless multimode cavities[J]. IEEE Journal of Quantum Electronics, 2004, 40(10): 1511-1518. doi: 10.1109/JQE.2004.834773 [104] RUAN ZH CH, FAN SH H. Temporal coupled-mode theory for light scattering by an arbitrarily shaped object supporting a single resonance[J]. Physical Review A, 2012, 85(4): 043828. doi: 10.1103/PhysRevA.85.043828 [105] KIKKAWA R, NISHIDA M, KADOYA Y. Polarization-based branch selection of bound states in the continuum in dielectric waveguide modes anti-crossed by a metal grating[J]. New Journal of Physics, 2019, 21(11): 113020. doi: 10.1088/1367-2630/ab4f54 [106] HSU C W, ZHEN B, CHUA S L, et al. Bloch surface eigenstates within the radiation continuum[J]. Light:Science &Applications, 2013, 2(7): e84. [107] SADRIEVA Z, FRIZYUK K, PETROV M, et al. Multipolar origin of bound states in the continuum[J]. Physical Review B, 2019, 100(11): 115303. doi: 10.1103/PhysRevB.100.115303 [108] WU P C, LIAO C Y, SAVINOV V, et al. Optical anapole metamaterial[J]. ACS Nano, 2018, 12(2): 1920-1927. doi: 10.1021/acsnano.7b08828 [109] POSHAKINSKIY A V, PODDUBNY A N. Optomechanical kerker effect[J]. Physical Review X, 2019, 9(1): 011008. doi: 10.1103/PhysRevX.9.011008 [110] SHAMKHI H K, BARYSHNIKOVA K V, SAYANSKIY A, et al. Transverse scattering and generalized kerker effects in all-dielectric mie-resonant metaoptics[J]. Physical Review Letters, 2019, 122(19): 193905. doi: 10.1103/PhysRevLett.122.193905 [111] SAVINOV V, FEDOTOV V A, ZHELUDEV N I. Toroidal dipolar excitation and macroscopic electromagnetic properties of metamaterials[J]. Physical Review B, 2014, 89(20): 205112. doi: 10.1103/PhysRevB.89.205112 [112] KAELBERER T, FEDOTOV V A, PAPASIMAKIS N, et al. Toroidal Dipolar response in a metamaterial[J]. Science, 2010, 330(6010): 1510-1512. doi: 10.1126/science.1197172 [113] FERNANDEZ-CORBATON I, NANZ S, ROCKSTUHL C. On the dynamic toroidal multipoles from localized electric current distributions[J]. Scientific Reports, 2017, 7(1): 7527. doi: 10.1038/s41598-017-07474-4 [114] MUN J, SO S, JANG J, et al. Describing meta-atoms using the exact higher-order polarizability tensors[J]. ACS Photonics, 2020, 7(5): 1153-1162. doi: 10.1021/acsphotonics.9b01776 [115] YIN X F, JIN J CH, SOLJAČIĆ M, et al. Observation of topologically enabled unidirectional guided resonances[J]. Nature, 2020, 580(7804): 467-471. doi: 10.1038/s41586-020-2181-4 [116] LIU W ZH, WANG B, ZHANG Y W, et al. Circularly polarized states spawning from bound states in the continuum[J]. Physical Review Letters, 2019, 123(11): 116104. doi: 10.1103/PhysRevLett.123.116104 [117] JIN J CH, YIN X F, NI L F, et al. Topologically enabled ultrahigh-Q guided resonances robust to out-of-plane scattering[J]. Nature, 2019, 574(7779): 501-504. doi: 10.1038/s41586-019-1664-7 [118] KANG M, ZHANG SH P, XIAO M, et al. Merging bound states in the continuum at off-high symmetry points[J]. Physical Review Letters, 2021, 126(11): 117402. doi: 10.1103/PhysRevLett.126.117402 [119] HWANG M S, LEE H C, KIM K H, et al. Ultralow-threshold laser using super-bound states in the continuum[J]. Nature Communications, 2021, 12(1): 4135. doi: 10.1038/s41467-021-24502-0 [120] CHEN Z H, YIN X F, JIN J CH, et al. Observation of miniaturized bound states in the continuum with ultra-high quality factors[J]. Science Bulletin, 2022, 67(4): 359-366. doi: 10.1016/j.scib.2021.10.020 [121] HAN S, CONG L Q, SRIVASTAVA Y K, et al. All-dielectric active terahertz photonics driven by bound states in the continuum[J]. Advanced Materials, 2019, 31(37): 1901921. doi: 10.1002/adma.201901921
下载:
