双路偏振结构的多普勒测速系统 -

姓名
邮箱
手机号码
标题
留言内容
验证码

双路偏振结构的多普勒测速系统

doi:10.37188/CO.2022-0211

陶善静^{1, 2,},
甄胜来^{1, 2,,},
方健^{1, 2},
陈鑫^{1, 2},
吕韬³,
俞本立^{1, 2}

1.
安徽大学光电信息获取与控制教育部重点实验室, 安徽合肥 230601
2.
安徽大学信息材料与智能感知安徽省实验室, 安徽合肥 230601
3.
安徽至博光电科技股份有限公司, 安徽合肥 230088

基金项目:安徽省重点研究与开发计划（No. 202104a05020059）；安徽省优秀科研创新团队（No. 2022AH010003）

详细信息

作者简介:
陶善静（1996—），男，安徽庐江人，硕士研究生，2020 年于安徽理工大学获得学士学位，主要从事光纤传感等方面的研究。E-mail：tao758501@163.com
甄胜来（1977—），男，安徽固镇人，博士，教授，硕士生导师，合肥市拔尖人才，芬兰Aalto大学访问学者，2008 年于安徽大学获得博士学位，主要从事于相干探测与光纤传感装置的研究。E-mail：slzhen@ahu.edu.cn

中图分类号:TN29
计量
- 文章访问数:310
- HTML全文浏览量:153
- PDF下载量:263
- 被引次数:0
出版历程
- 收稿日期:2022-10-11
- 录用日期:2023-01-18
- 修回日期:2022-11-11
- 网络出版日期:2023-03-08

Laser Doppler velocimetry with a dual polarization structure

TAO Shan-jing^{1, 2,},
ZHEN Sheng-lai^{1, 2,,},
FANG Jian^{1, 2},
CHEN Xin^{1, 2},
LV Tao³,
YU Ben-Li^{1, 2}

1.
Key-Laboratory of Opto-Electronic Information Acquisiton and Manipulation, Ministry of Education, Anhui University, Hefei 230601, China
2.
Information Materials and Intelligent Sensing-Laboratory of Anhui Province, Anhui University, Hefei 230601, China
3.
Anhui Zhibo Optoelectronic Technology Co., Ltd, Hefei 230088, China

Funds:Supported by Key Research and Development Plan of Anhui Province (No. 202104a05020059); Excellent Scientific Research and Innovation Team of Anhui Province (No. 2022AH010003)

More Information

Corresponding author:slzhen@ahu.edu.cn

摘要

摘要:
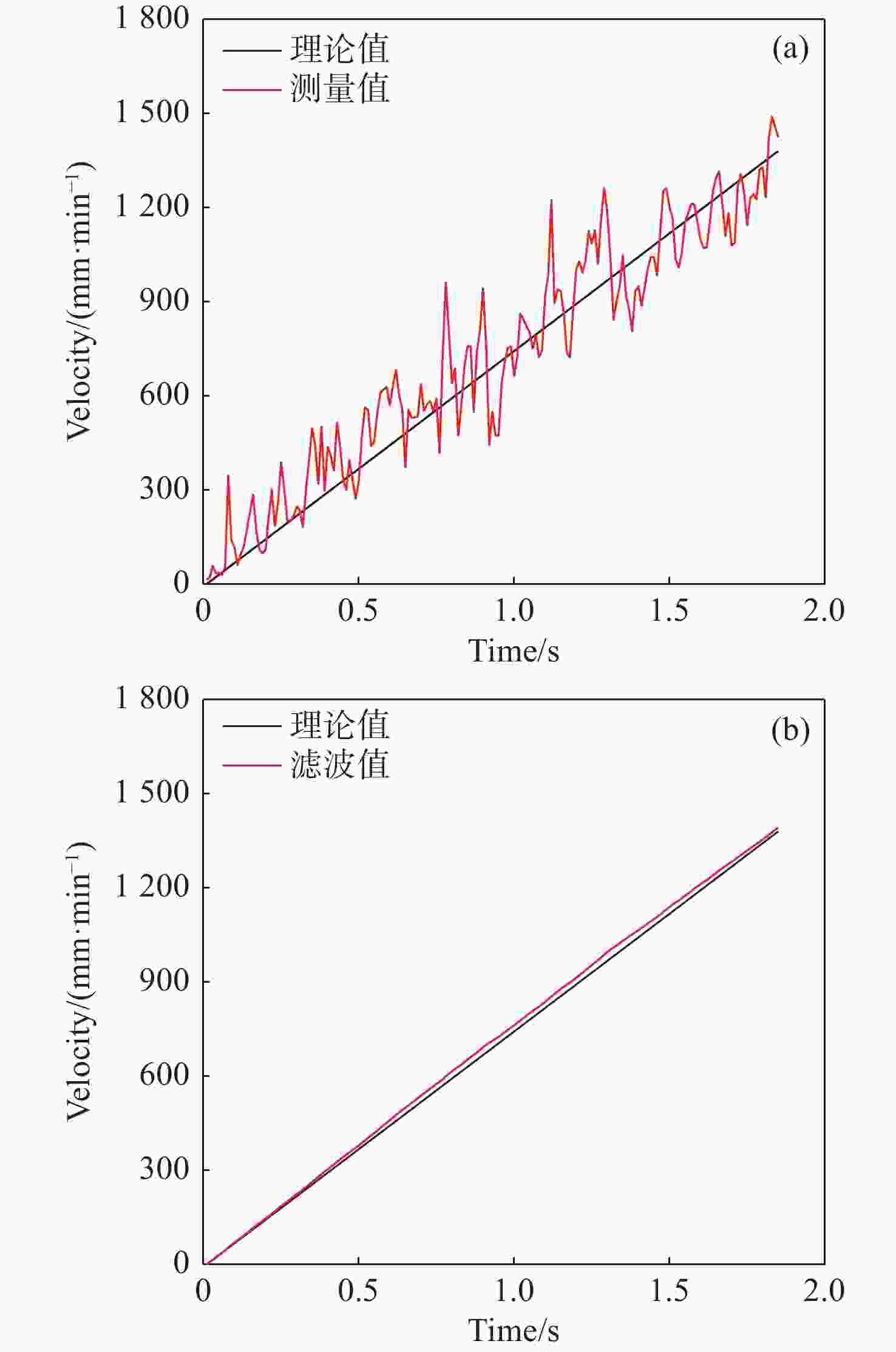
为了消除光束倾角带来的不确定性，本文建立了一种双路偏振式多普勒测速系统。该系统使用双光束双探头结构来探测物体的运动信息。首先，通过转动实验精确获得双光束间的夹角大小，对于任意光束倾角，本文采用双探头装置收集运动物体表面的散射光束，结合双路偏振式光路结构，得到两路干涉信号的多普勒频移。然后，创新性采用了细化分帧算法对两路干涉信号进行实时解调，通过两路速度分量的合成得到物体真实速度。实验结果表明：速度在10 mm/min~1500 mm/min范围内，测量值与理论值之间的平均误差可以达到1%~5%。在非平稳运动过程中，通过细化分帧算法修正后的v-t图像RMSE均值为1.19 mm/min。该系统结构满足速度测量的稳定可靠、精度高、抗干扰能力强等要求。
- 多普勒测速/
- 双路偏振/
- 细化分帧/
- 双探头
Abstract:
In order to eliminate the uncertainty caused by the inclination of a beam, a dual polarization laser Doppler velocimetry system is established. We use a structure with two beams and two probes to detect the motion of the object. Firstly, the angle between the two beams is obtained by a calibration experiment. For any beam inclination, the scattered beam on the surface of a moving object is collected by a dual-probe device, and the Doppler shift of the two interference signals is obtained by combining the dual polarization optical path structure. Then, the refined framing algorithm is applied to demodulate the two interference signals in real time. The real speed of the object is obtained through the synthesis of the two speed components. The experimental results show that the average deviation between the measured value and the theoretical value can reach 1%−5% when the speed is within the range of 10 mm/min~1500 mm/min. In the process of non-stationary motion, the mean RMSE of the v-t image corrected by the refining frame segmentation algorithm is 1.19 mm/min. The system’s structure meets the requirements of stability and reliability, high precision and strong anti-interference ability in speed measurement.
- Laser Doppler Velocimetry(LDV)/
- dual polarization/
- refine framing/
- double probe

HTML全文

图 1 多普勒测速原理示意图

Figure 1.Schematic diagram of laser doppler velocimetry principle

下载: 全尺寸图片幻灯片

图 2光路系统图

Figure 2.Structure diagram of optical system

下载: 全尺寸图片幻灯片

图 3光束与目标物之间的细节图

Figure 3.Detail between the beam and the target

下载: 全尺寸图片幻灯片

图 4信号采集图。（a）原始信号；（b）200 K~280 K处采样点；（c）280 K~300 K处采样点；（d）原始信号频谱

Figure 4.Signal acquisition diagram. (a) Original signal; (b) sampling points at 200 K~280 K; (c) sampling points at 280 K~300 K; (d) original signal spectrum

下载: 全尺寸图片幻灯片

图 5信号处理流程图

Figure 5.Signal processing flow chart

下载: 全尺寸图片幻灯片

图 6光路实物图

Figure 6.Physical picture of the optical path

下载: 全尺寸图片幻灯片

图 7（a）1路和（b）2路原始信号图

Figure 7.Original signal diagrams of (a) channel 1 and (b) channel 2

下载: 全尺寸图片幻灯片

图 8（a）1路和（b）2路信号的频谱图

Figure 8.Spectrum diagrams of signals in (a) channel 1 and (b) channel 2

下载: 全尺寸图片幻灯片

图 9（a） FFT 对数振幅谱及（b）细化分帧对数振幅谱

Figure 9.(a) FFT logarithmic amplitude spectrum and (b) refine framing logarithmic amplitude spectrum

下载: 全尺寸图片幻灯片

图 10不同分帧下的时频图。（a）N=5 K；（b）N=2 K；（c）N=1 K；（d）N=0.5 K；（e）N=0.25 K；（f）N=0.2 K；

Figure 10.Time frequency diagrams under different framings. (a)N=5 K; (b)N=2 K; (c)N=1 K; (d)N=0.5 K; (e)N=0.25 K; (f)N=0.2 K；

下载: 全尺寸图片幻灯片

图 11光束夹角的变化情况

Figure 11.Change in beam’s angle

下载: 全尺寸图片幻灯片

图 12（a）1路和（b）2路速度分量与（c）合速度

Figure 12.Speed component of (a) channel 1 and (b) channel 2 and (c) the combined speed

下载: 全尺寸图片幻灯片

图 13（a）细化分帧解调后和（b）STFT解调后的v-t图

Figure 13.Detailed v-t diagram after (a) frame dividing demodulation and (b) STFT demodulation

下载: 全尺寸图片幻灯片

图 14不同倾角下的速度测量值

Figure 14.Velocity measurement values at different beam angles

下载: 全尺寸图片幻灯片

图 15加速过程中（a）1路，（b）2 路和（c）合速度的v-t图像

Figure 15.v-t diagram of (a) channel 1; (b) channel 2 and (c) the combined speed during acceleration

下载: 全尺寸图片幻灯片

图 16（a）未经算法修正和（b）算法修正后结果

Figure 16.v-t diagram (a) before and (b) after algorithm modification

下载: 全尺寸图片幻灯片

图 17滤波前后的均方根误差对比图

Figure 17.Comparison of RMSE before and after filtering

下载: 全尺寸图片幻灯片

表 1速度测量的结果对比

Table 1.Comparison results of speed measurement

线性位移平台速度 (mm/min)	细化分帧				STFT
线性位移平台速度 (mm/min)	APD1 (Hz)	APD2 (Hz)	和速度 (mm/min)	偏差 (%)	APD1 (Hz)	APD2 (Hz)	和速度 (mm/min)	偏差 (%)
1500	13524	11915	1482	1.20	13478	11959	1414	5.73
1200	10827	9550	1215	1.25	10878	9661	1134	5.50
1000	9186	8086	1014	1.40	9074	8060	946	5.40
800	7309	6427	810	1.27	7305	6523	726	9.25
600	5490	4824	611	1.88	5417	4819	558	7.00

下载: 导出CSV

参考文献 (24)

[1]	YEH Y, CUMMINS H Z. Localized fluid flow measurements with an He-Ne laser spectrometer[J].Applied Physics Letters, 1964, 4(10): 176-178.doi:10.1063/1.1753925
[2]	OJO A O, FOND B, VAN WACHEM B G M,et al. Thermographic laser Doppler velocimetry[J].Optics Letters, 2015, 40(20): 4759-4762.doi:10.1364/OL.40.004759
[3]	BOU E, LY A, ROUL J,et al. Compact system forin situlaser Doppler velocimetry of blood flow[J].Biomedical Optics Express, 2019, 10(11): 5862-5876.doi:10.1364/BOE.10.005862
[4]	武颖丽, 吴振森. 基于希尔伯特变化的微小振动多普勒信号处理[J]. 中国光学,2013,6(3):415-420. WU Y L, WU ZH S. Micro-vibration laser Doppler signal processing based on Hilbert transform[J].China Optics, 2013, 6(3): 415-420. (in Chinese)
[5]	ROSS M M. Combined differential and reference beam LDV for 3D velocity measurement[J].Optics and Lasers in Engineering, 1997, 27(6): 587-619.doi:10.1016/S0143-8166(96)00065-6
[6]	李秀明, 黄战华, 朱猛. 扩展光束型多普勒速度测量系统[J]. 光学精密工程,2013,21(5):1102-1109.doi:10.3788/OPE.20132105.1102 LI X M, HUANG ZH H, ZHU M. Differential laser Doppler system with expanded beams for velocity measurement[J].Optics and Precision Engineering, 2013, 21(5): 1102-1109. (in Chinese)doi:10.3788/OPE.20132105.1102
[7]	闫亚东, 何俊华, 许瑞华, 等. 聚变冲击波被动式测速光学系统设计[J]. 光学精密工程,2018,26(11):2662-2668.doi:10.3788/OPE.20182611.2662 YAN Y D, HE J H, XU R H,et al. Optical system for passive laser fusion shock wave velocity measurement[J].Optics and Precision Engineering, 2018, 26(11): 2662-2668. (in Chinese)doi:10.3788/OPE.20182611.2662
[8]	赵洪博. 基于多普勒效应的速度信号探测与频率解算算法研究[D]. 青岛: 青岛科技大学, 2019. ZHAO H B. Research on speed signal detection and frequency algorithm based on Doppler effect[D]. Qingdao: Qingdao University of Science & Technology, 2019. (in Chinese)
[9]	JIAN ZH, LONG X W. Laser Doppler velocimeter using a single longitudinal mode solid-state laser source[J].Optics&Laser Technology, 2010, 42(7): 1167-1171.
[10]	CHEN J B, WANG X M, WU Y B,et al. Ultralow Doppler frequency extraction for the self-mixing dual-frequency laser velocimetry[J].Applied Optics, 2022, 61(16): 4687-4692.doi:10.1364/AO.455671
[11]	GENG Y H, JIANG CH L, KAN L L. Enhanced laser self-mixing Doppler velocity measurement with pre-feedback mirror[J].Applied Optics, 2019, 58(27): 7571-7576.doi:10.1364/AO.58.007571
[12]	李芝绒, 王胜强, 潘文. 双光束差动多普勒测速法在高冲击校准技术中的应用[J]. 计测技术,2013,33(4):21-25.doi:10.3969/j.issn.1674-5795.2013.04.004 LI ZH R, WANG SH Q, PAN W. Application of double beam differential laser Doppler velocimetry in high g impact calibration technology[J].Metrology&Measurement Technology, 2013, 33(4): 21-25. (in Chinese)doi:10.3969/j.issn.1674-5795.2013.04.004
[13]	ALEXANDROVA A S, TZOGANIS V, WELSCH C P. Laser diode self-mixing interferometry for velocity measurements[J].Optical Engineering, 2015, 54(3): 034104.doi:10.1117/1.OE.54.3.034104
[14]	FISCHER A. Limiting uncertainty relations in laser-based measurements of position and velocity due to quantum shot noise[J].Entropy, 2019, 21(3): 264.doi:10.3390/e21030264
[15]	XIANG ZH Y, WANG Q, HUANG R,et al. Position observation-based calibration method for an LDV/SINS integrated navigation system[J].Applied Optics, 2021, 60(26): 7869-7877.doi:10.1364/AO.430866
[16]	MARU K, YOSHIDA Y, YUKINARI M,et al. Differential laser Doppler velocimetry for cross-sectional velocity distribution measurements using 48-channel spatial encoding and nonmechanical scanning[J].Optical Review, 2019, 26(5): 487-492.doi:10.1007/s10043-019-00544-0
[17]	DE GEVIGNEY M D. Novel surface scanning inspection system for opaque and transparent substrates using laser Doppler velocimetry[C].Proceedingsofthe29thAnnualSEMIAdvancedSemiconductorManufacturingConference(ASMC), IEEE, 2018: 23-28.
[18]	FAN ZH, SUN Q, DU L,et al. Janus‐configured all fibre laser Doppler velocimetry[J].IET Optoelectronics, 2018, 12(1): 50-54.doi:10.1049/iet-opt.2017.0047
[19]	周健, 龙兴武. 基于Janus配置的多普勒测速仪[J]. 光电子· ,2011,22(2):266-271. ZHOU J, LONG X W. Laser Doppler velocimeter based on Janus configuration[J].Journal of Optoelectronics·Laser, 2011, 22(2): 266-271. (in Chinese)
[20]	张艳艳, 巩轲, 何淑芳, 等. 多普勒测速技术进展[J]. 与红外,2010,40(11):1157-1162.doi:10.3969/j.issn.1001-5078.2010.11.001 ZHANG Y Y, GONG K, HE SH F,et al. Progress in laser Doppler velocity measurement techniques[J].Laser&Infrared, 2010, 40(11): 1157-1162. (in Chinese)doi:10.3969/j.issn.1001-5078.2010.11.001
[21]	孙端. 短时傅里叶变换在工业测量中的应用[J]. 机电信息,2020(26):14-15.doi:10.3969/j.issn.1671-0797.2020.26.007 SUN D. Application of short time Fourier transform in industrial measurement[J].Mechanical and Electrical Information, 2020(26): 14-15. (in Chinese)doi:10.3969/j.issn.1671-0797.2020.26.007
[22]	HUANG D, LIU J, DENG L J,et al. An adaptive Kalman filter for online monitoring of mine wind speed[J].Archives of Mining Sciences, 2019, 64(4): 813-827.
[23]	周金男, 邬战军, 范哲, 等. 车载多普勒测速仪的卡尔曼滤波算法研究[J]. 中国 ,2014,41(11):1102006.doi:10.3788/CJL201441.1102006 ZHOU J N, WU ZH J, FAN ZH,et al. Research on Kalman filter algorithm for vehicle laser Doppler velocimeter[J].Chinese Journal of Lasers, 2014, 41(11): 1102006. (in Chinese)doi:10.3788/CJL201441.1102006
[24]	王广玉, 窦磊, 窦杰. 基于自适应卡尔曼滤波的多目标跟踪算法[J]. 计算机应用,2022,42(S1):271-275. WANG G Y, DOU L, DOU J. Multiple object tracking algorithm based on adaptive Kalman filter[J].Journal of Computer Applications, 2022, 42(S1): 271-275. (in Chinese)