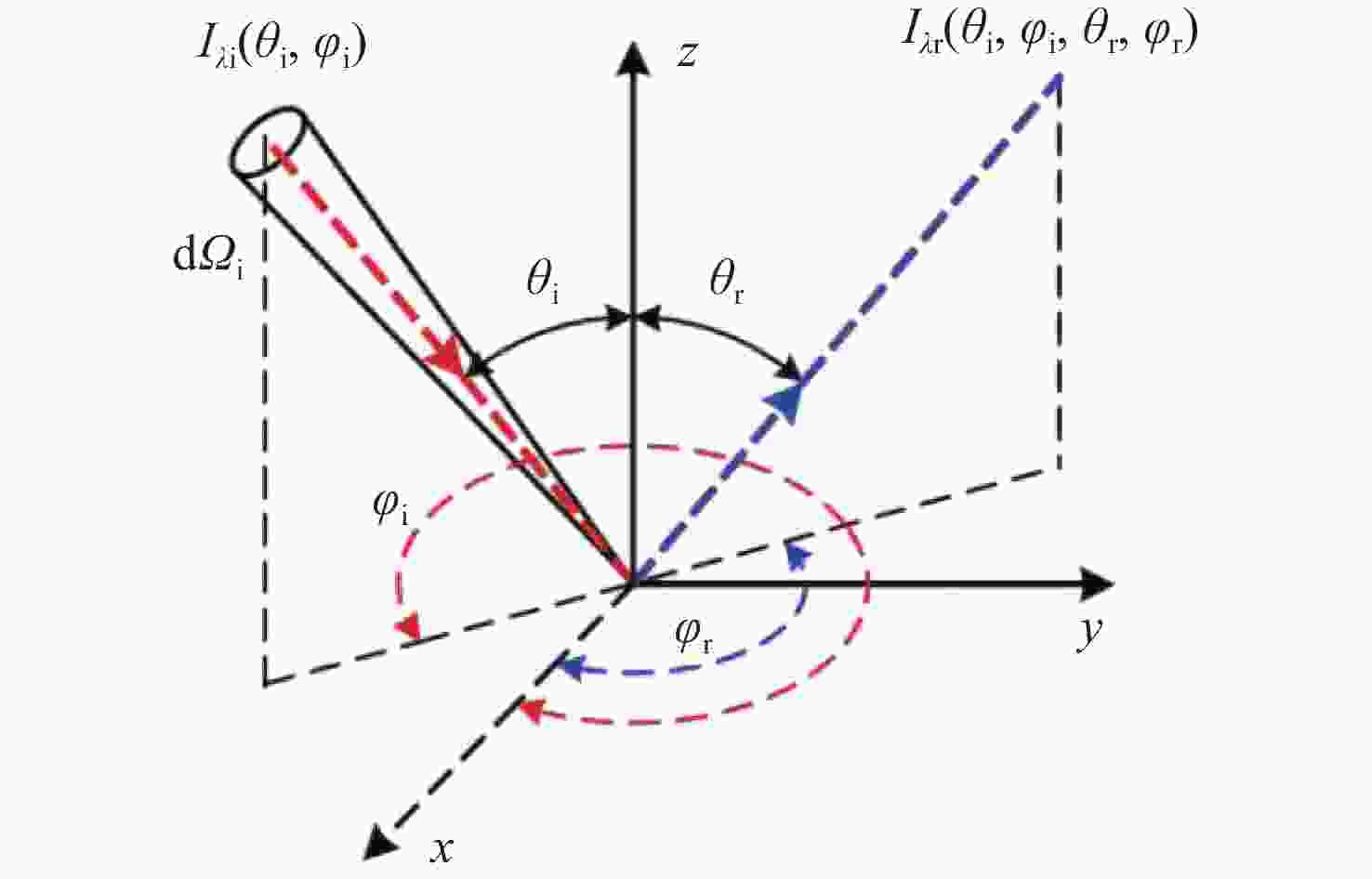
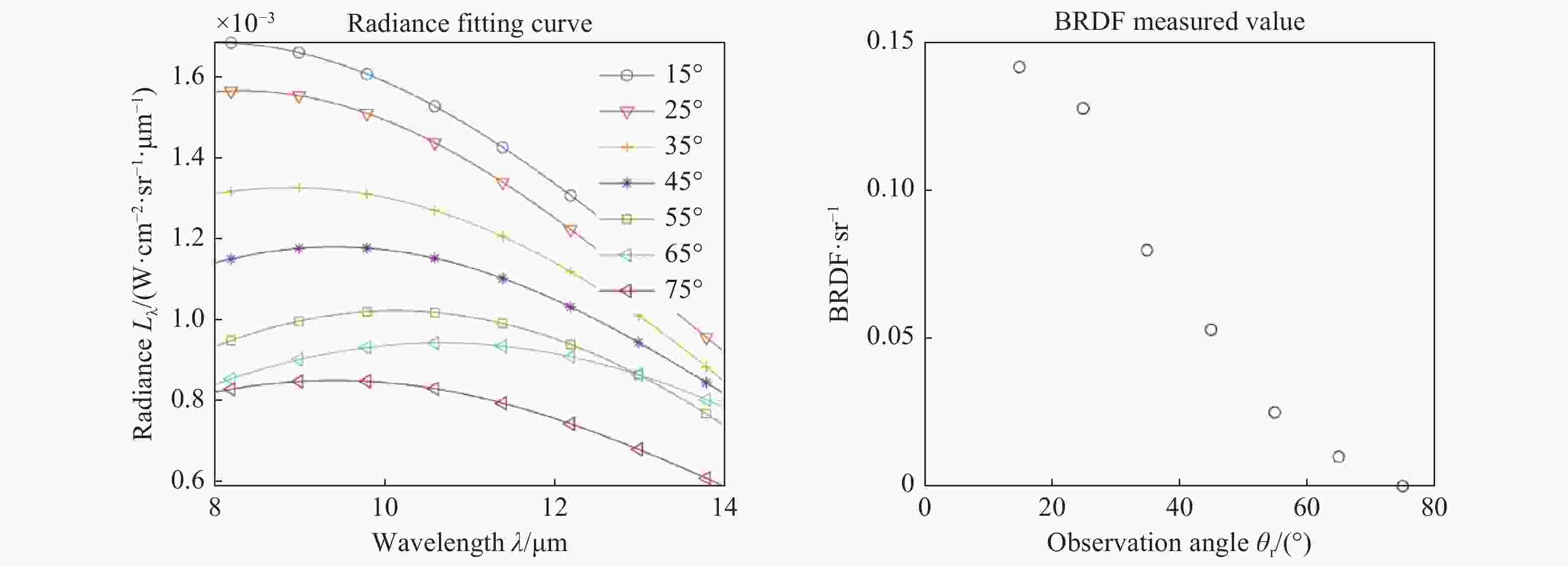
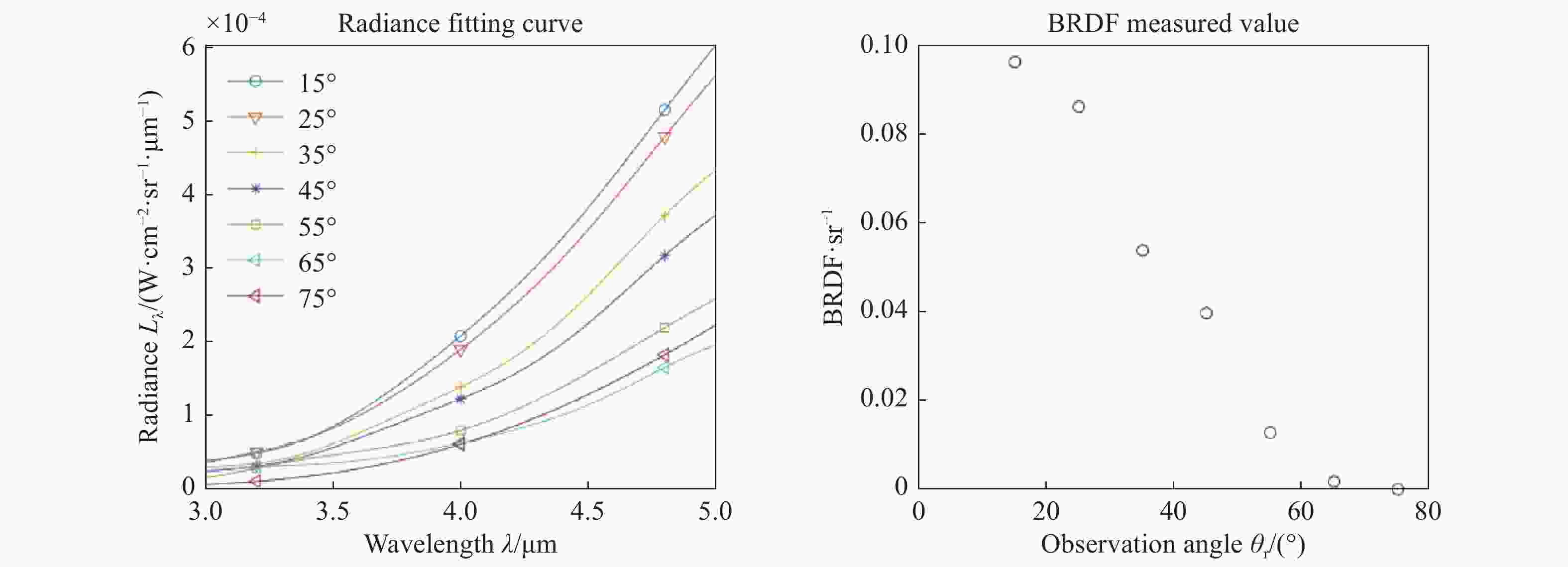
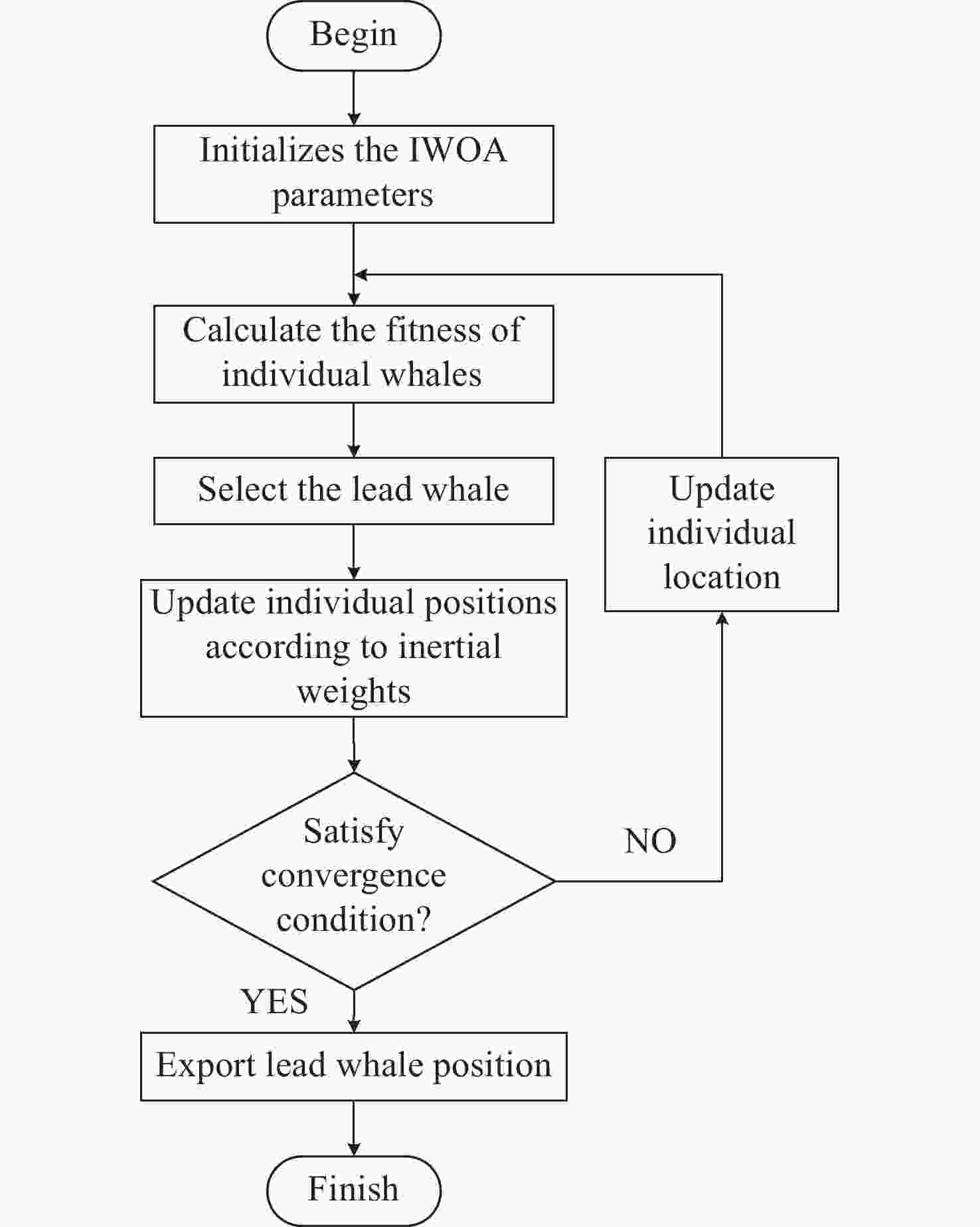
Infrared reflection characteristics of the wall solved by improved whale optimization algorithm
-
摘要:
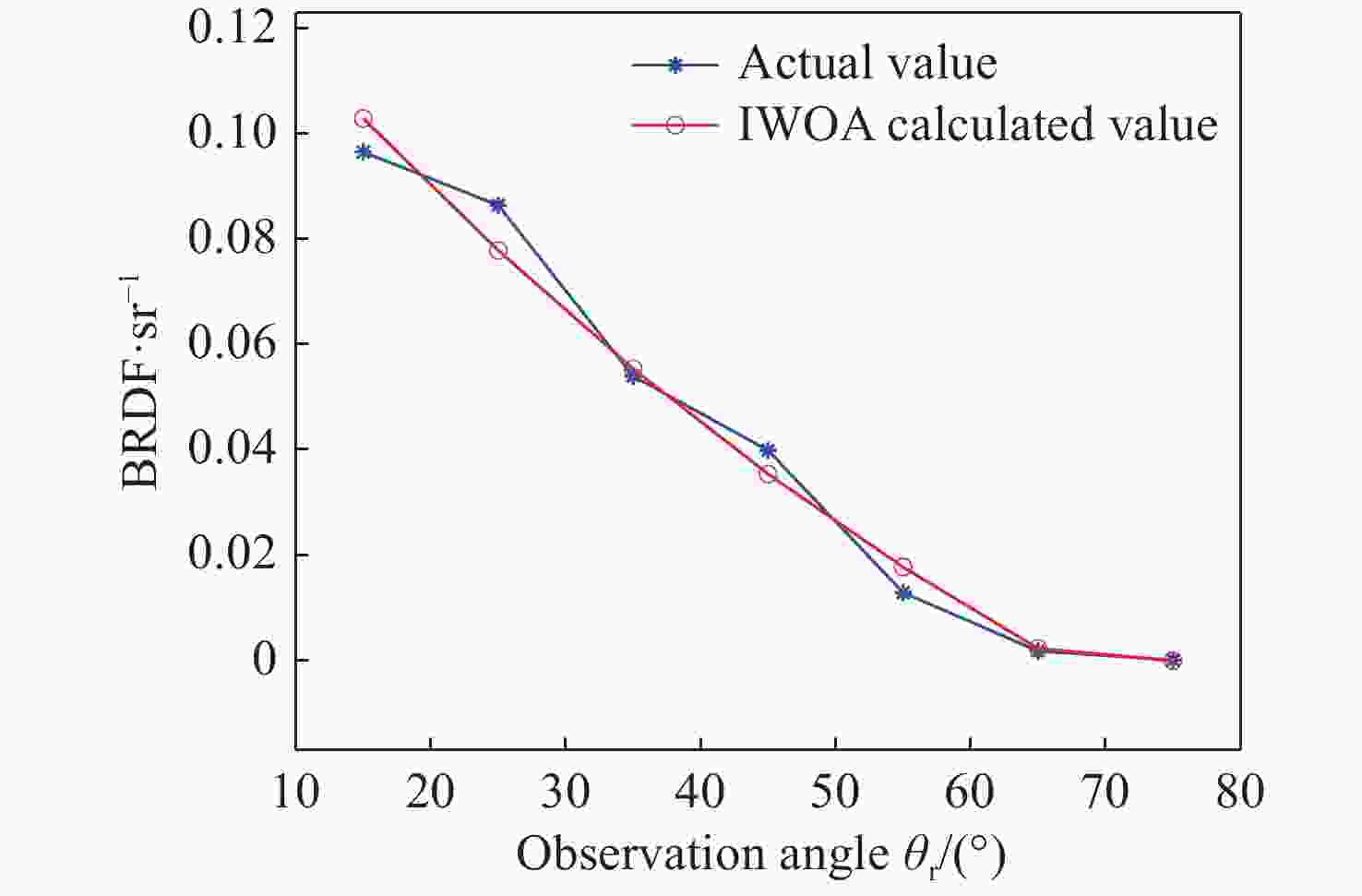
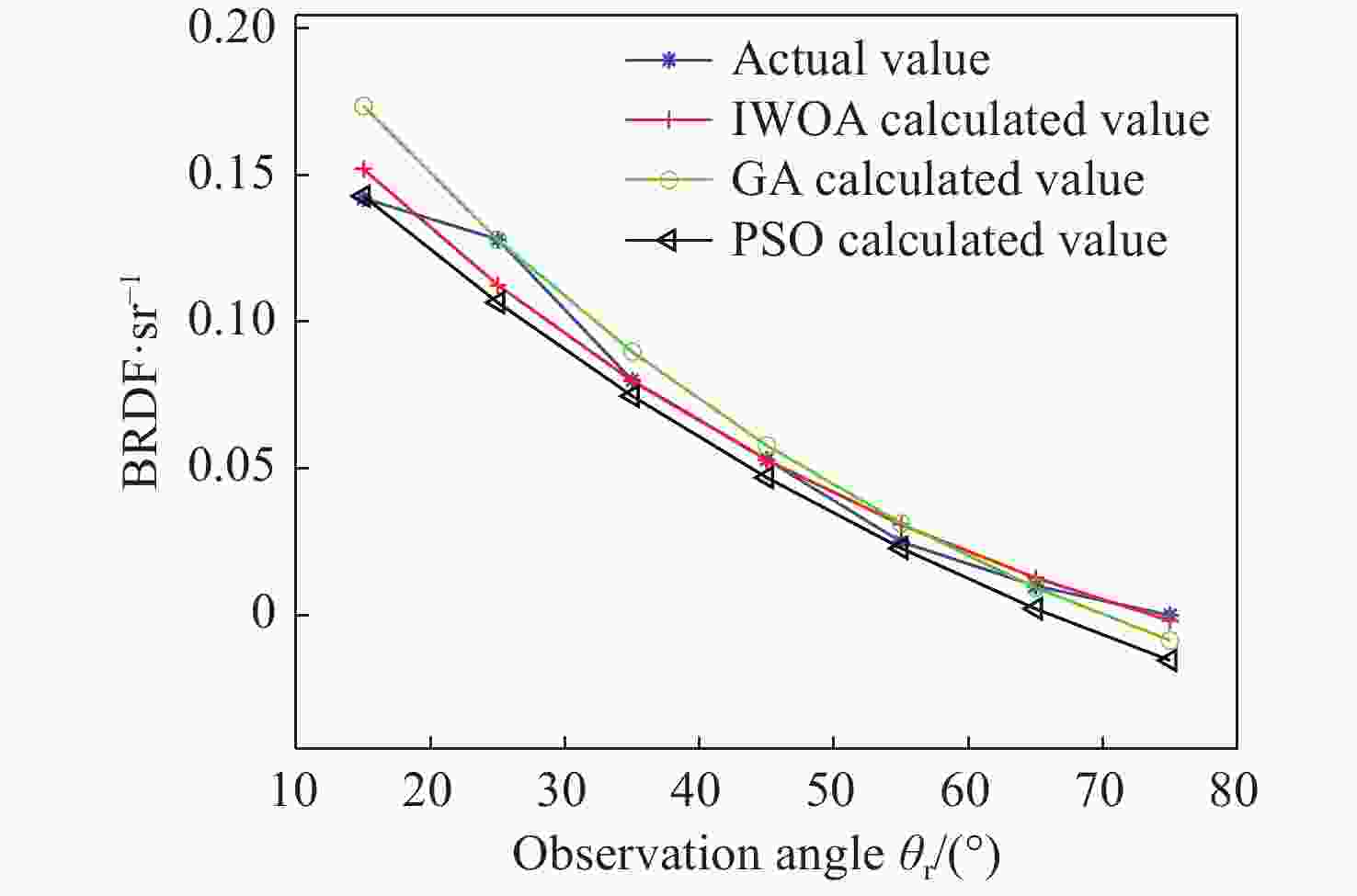
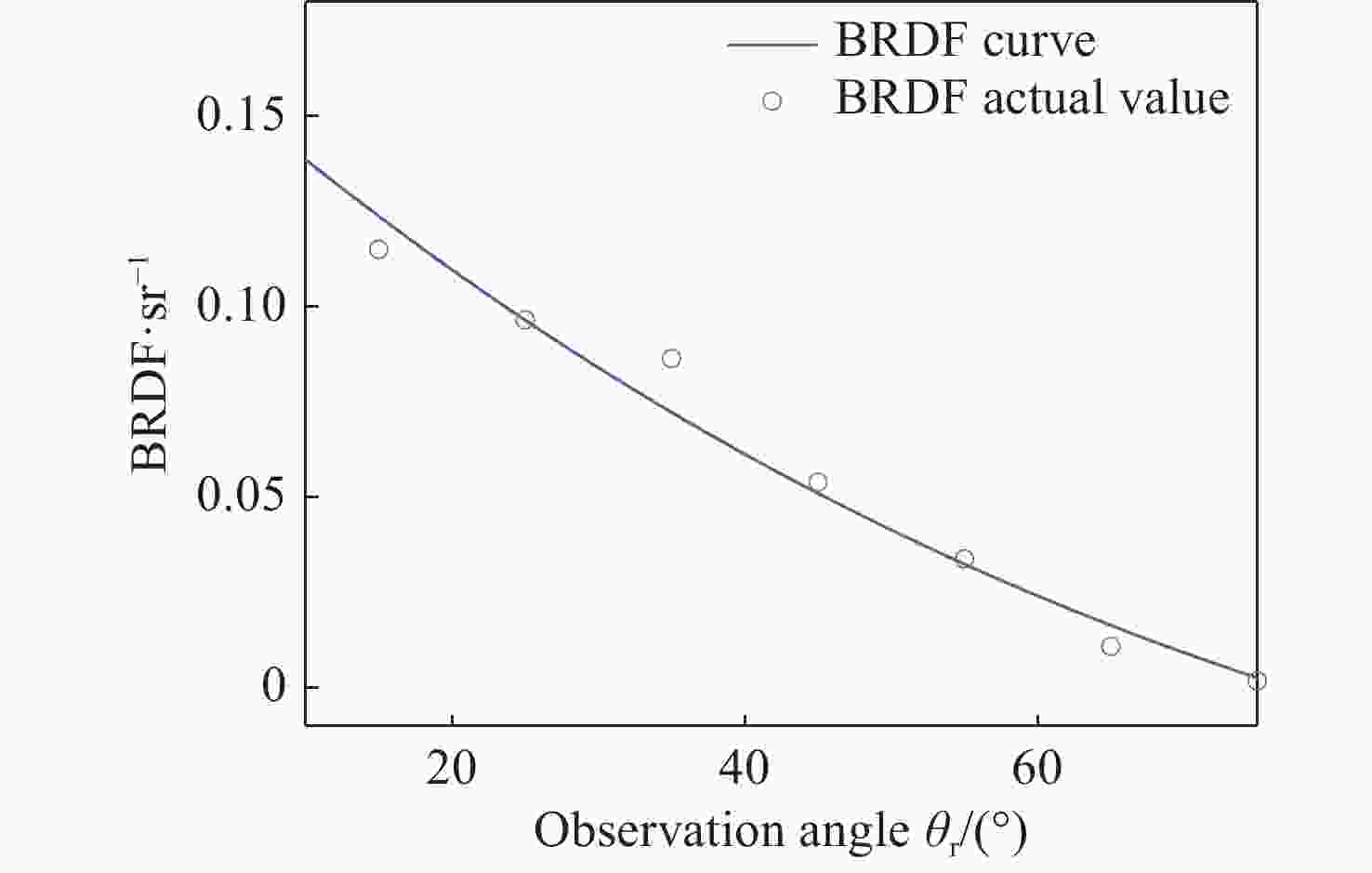
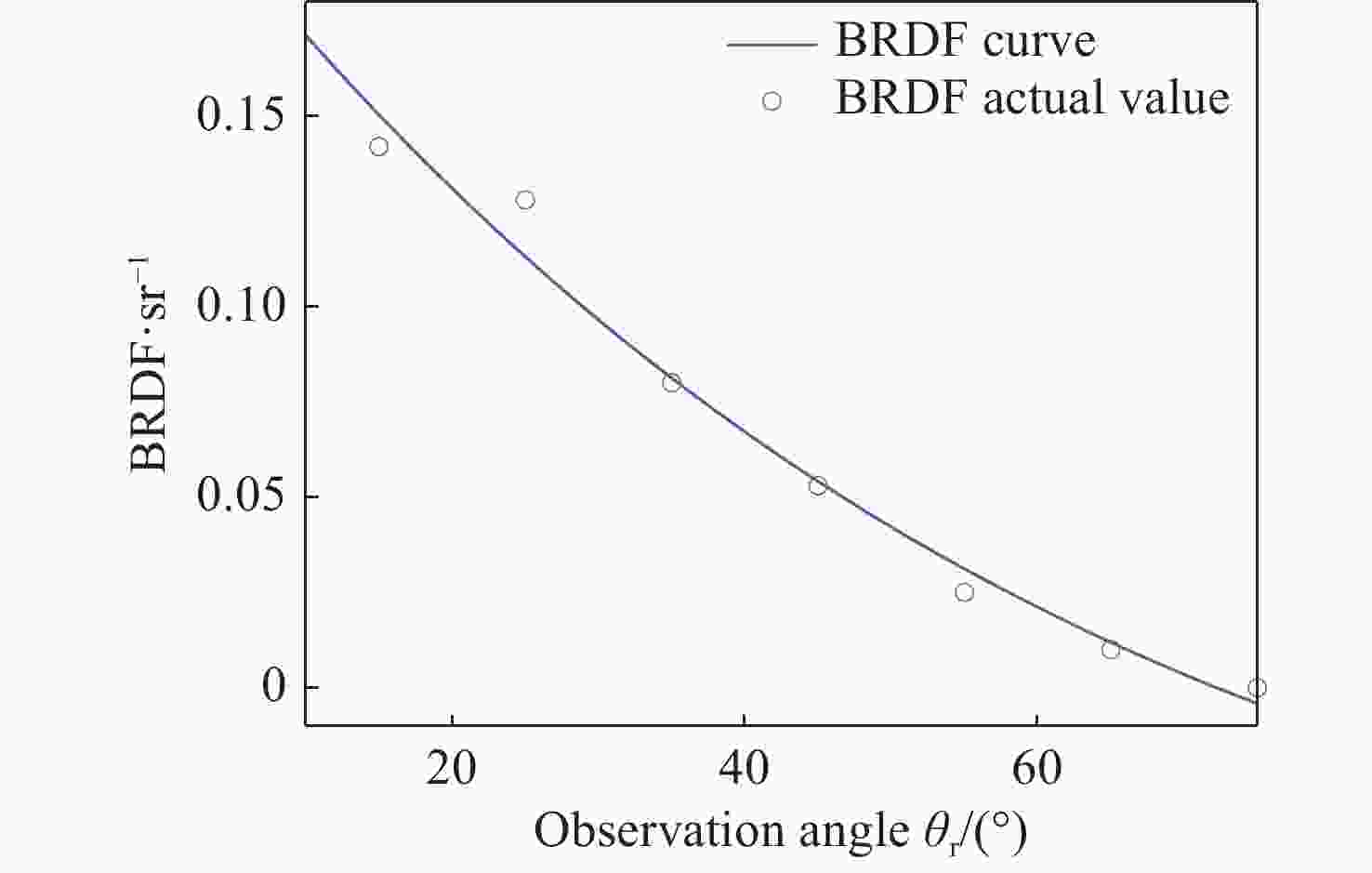
壁面的红外反射特性由双向反射分布函数(BRDF)表征和求解。目前BRDF测量需要大量实验数据，同时存在精度不高的问题。通过构建壁面反射特性测试平台，使用MR170型傅立叶红外光谱辐射计获取2~15 μm波段下入射角度和各个反射角度的目标辐射亮度。针对隐身目标，应用RBF网络对3~5 μm以及8~14 μm波段的辐射亮度曲线进行拟合，排除大气干扰，进而求解出上述两个波段隐身目标的BRDF值。为了解决BRDF模型精度不高的问题，提出了改进的鲸鱼优化算法(IWOA)，对BRDF模型参数进行反演，并设计了基于BRDF的反射率求解方法。IWOA对BRDF计算模型参数反演有良好的效果。根据反射法，应用所得到的BRDF数据求解得到的反射率为0.5496，相对误差为6.17%，满足工程需求。
-
关键词:
- 双向反射分布函数(BRDF) /
- 鲸鱼优化算法 /
- 辐射亮度 /
- 参数反演
Abstract:The infrared reflection characteristics of the wall are characterized and solved by the bidirectional reflectance distribution function (BRDF). BRDF measurement currently has two problems to be addressed: it requires much experimental data and accuracy is not high enough. By constructing the reflection characteristic test platform of the wall target, an MR170 Fourier infrared spectroradiometer was used to obtain the target radiance at the incident angle and each reflection angle in the 2−15 μm band. For the stealth target, the RBF network was used to fit the radiance at the bands of 3−5 μm and 8−14 μm to eliminate atmospheric interference. Then, the BRDF values of the stealth targets in the above two bands were obtained. To improve the accuracy of the BRDF model, an improved whale optimization algorithm (IWOA) was proposed to invert BRDF model parameters, and a reflectivity-solving method based on BRDF was designed. The IWOA has a good effect on the parameter inversion of the BRDF calculation model. According to the reflection method and applying the obtained BRDF data, the reflectance 0.5496 and the relative error 6.17% are obtained, which meet the engineering requirements.
-
图 1 不同介质表面反射特性示意图
Figure 1. Schematic diagram of the surface reflection properties of the different media
图 4 3~5 μm波段反射亮度及BRDF测量值
Figure 4. Reflection brightness and BRDF measurements in 3~5 μm bands
图 5 8~14 μm反射亮度及BRDF测量值
Figure 5. Reflection brightness and BRDF measurements in 8~14 μm bands
图 6 座头鲸螺旋上升捕食方法示意图
Figure 6. Schematic diagram of the humpback whale's ascending spiral predation method
图 8 3~5 μm波段IWOA模型改进效果图
Figure 8. Improved effect of the IWOA model in the 3~5 μm band
图 9 3~5 μm波段IWOA模型反演结果对比
Figure 9. Comparison of the inversion results of the IWOA model in the 3~5 μm band
图 10 8~14 μm波段IWOA模型反演结果对比
Figure 10. Comparison of the inversion results of the IWOA model in the 8~14 μm band
图 11 3~5 μm波段3种算法反演结果与真实值对比
Figure 11. Comparison of the inversion results of three algorithms and actual values in the 3~5 μm band
图 12 8~14 μm波段3种算法反演结果与真实值对比
Figure 12. Comparison of the inversion results of three algorithms and actual values in the 8~14 μm band
图 15 光源垂直入射目标壁面的反射亮度包线
Figure 15. The reflected brightness envelope when the light source incidents vertically on the wall
表 1 误差计算结果
Table 1. Error calculation results
误差函数 3~5 μm IWOA GA PSO MAE(10−3) 4.4 8 7.5 R2 0.9828 0.9494 0.9606 8~14 μm MAE(10−3) 6.1 10.3 9.8 R2 0.9797 0.9369 0.9574 
下载: 导出CSV
-
[1] NICODEMUS F E. Reflectance nomenclature and directional reflectance and emissivity[J]. Applied Optics, 1970, 9(6): 1474-1475. doi: 10.1364/AO.9.001474 [2] 宿德志, 刘亮, 吴世永, 等. 辐射耦合效应对目标红外偏振特性的影响[J]. 中国光学(中英文),2023,16(2):318-328. doi: 10.37188/CO.2022-0035SU D ZH, LIU L, WU SH Y, et al. Influence of radiation coupling effect on polarization characteristics of targets[J]. Chinese Optics, 2023, 16(2): 318-328. doi: 10.37188/CO.2022-0035 [3] SCHLICK C. A customizable reflectance model for everyday rendering[C]. Proceedings of the Fourth Eurographics Workshop on Rendering, 1993. [4] PHONG B T. Illumination for computer generated pictures[J]. Communications of the ACM, 1975, 18(6): 311-317. doi: 10.1145/360825.360839 [5] COOK R L, TORRANCE K E. A reflectance model for computer graphics[C]. Proceedings of the 8th Annual Conference on Computer Graphics and Interactive Techniques, ACM, 1981: 307-316,doi: 10.1145/800224.806819. [6] 李铁, 王航宇, 王宏军. 目标表面BRDF统计建模中的遗传模拟退火算法[J]. 量子电子学报,2008,25(4):489-492. doi: 10.3969/j.issn.1007-5461.2008.04.019LI T, WANG H Y, WANG H J. Application of genetic simulated annealing algorithm in BRDF statistical modelling[J]. Chinese Journal of Quantum Electronics, 2008, 25(4): 489-492. doi: 10.3969/j.issn.1007-5461.2008.04.019 [7] 吴振森, 谢东辉, 谢品华, 等. 粗糙表面 散射统计建模的遗传算法[J]. 光学学报,2002,22(8):897-901. doi: 10.3321/j.issn:0253-2239.2002.08.001WU ZH S, XIE D H, XIE P H, et al. Genetic algorithm for statistical modeling of laser scattering on rough surface[J]. Acta Optica Sinica, 2002, 22(8): 897-901. doi: 10.3321/j.issn:0253-2239.2002.08.001 [8] 杨玉峰, 吴振森, 曹运华. 一种实用型粗糙面六参数双向反射分布函数模型[J]. 光学学报,2012,32(2):0229001. doi: 10.3788/AOS201232.0229001YANG Y F, WU ZH S, CAO Y H. Practical six-parameter bidirectional reflectance distribution function model for rough surface[J]. Acta Optica Sinica, 2012, 32(2): 0229001. (in Chinese). doi: 10.3788/AOS201232.0229001 [9] 杨敏, 方勇华, 吴军, 等. 基于Kubelka-Munk理论的涂层表面多参量偏振双向反射分布函数模型[J]. 光学学报,2018,38(1):0126002. doi: 10.3788/AOS201838.0126002YANG M, FANG Y H, WU J, et al. Multiple-component polarized bidirectional reflectance distribution function model for painted surfaces based on Kubelka-Munk theory[J]. Acta Optica Sinica, 2018, 38(1): 0126002. (in Chinese). doi: 10.3788/AOS201838.0126002 [10] 李明哲, 赵继广, 杨帆. 基于统计与遗传算法的Cook-Torrance模型研究[J]. 装备学院学报,2016,27(1):116-121. doi: 10.3783/j.issn.2095-3828.2016.01.024LI M ZH, ZHAO J G, YANG F. Analysis on cook-Torrance model based on genetic algorithm and statistical method[J]. Journal of Equipment Academy, 2016, 27(1): 116-121. doi: 10.3783/j.issn.2095-3828.2016.01.024 [11] 孙建平, 齐宏, 王申领, 等. 随机惯性权重微粒群算法的BRDF参数反演[J]. 杂志,2021,42(2):5-9. doi: 10.14016/j.cnki.jgzz.2021.02.005SUN J P, QI H, WANG SH L, et al. BRDF parameter inversion based on the stochastic inertia weight particle swarm optimization algorithm[J]. Laser Journal, 2021, 42(2): 5-9. doi: 10.14016/j.cnki.jgzz.2021.02.005 [12] LIU Y Y, DAI J J, ZHAO S S, et al. Optimization of five-parameter BRDF model based on hybrid GA-PSO algorithm[J]. Optik, 2020, 219: 164978. doi: 10.1016/j.ijleo.2020.164978 [13] MIRJALILI S, LEWIS A. The whale optimization algorithm[J]. Advances in Engineering Software, 2016, 95: 51-67. doi: 10.1016/j.advengsoft.2016.01.008 [14] 罗一甲, 祝赫, 李潇涵, 等. 赤霞珠酿酒葡萄总酚含量的近红外光谱定量分析[J]. 光谱学与光谱分析,2021,41(7):2036-2042. doi: 10.3964/j.issn.1000-0593(2021)07-2036-07LUO Y J, ZHU H, LI X H, et al. Quantitative analysis of total phenol content in cabernet sauvignon grape based on near-infrared spectroscopy[J]. Spectroscopy and Spectral Analysis, 2021, 41(7): 2036-2042. doi: 10.3964/j.issn.1000-0593(2021)07-2036-07 [15] DING H Q, WU ZH Y, ZHAO L CH. Whale optimization algorithm based on nonlinear convergence factor and chaotic inertial weight[J]. Concurrency and Computation:Practice and Experience, 2020, 32(24): e5949. doi: 10.1002/cpe.5949 [16] ADITYA SHASTRY K, SANJAY H A. A modified genetic algorithm and weighted principal component analysis based feature selection and extraction strategy in agriculture[J]. Knowledge-Based Systems, 2021, 232: 107460. doi: 10.1016/j.knosys.2021.107460 [17] ZHANG X M, LIN Q Y. Three-learning strategy particle swarm algorithm for global optimization problems[J]. Information Sciences, 2022, 593: 289-313. doi: 10.1016/j.ins.2022.01.075 -
下载:
计量
- 文章访问数: 230
- HTML全文浏览量: 93
- PDF下载量: 46
- 被引次数: 0
