Nonlinear error active coding optimal estimation correction method for fringe projection
-
摘要:
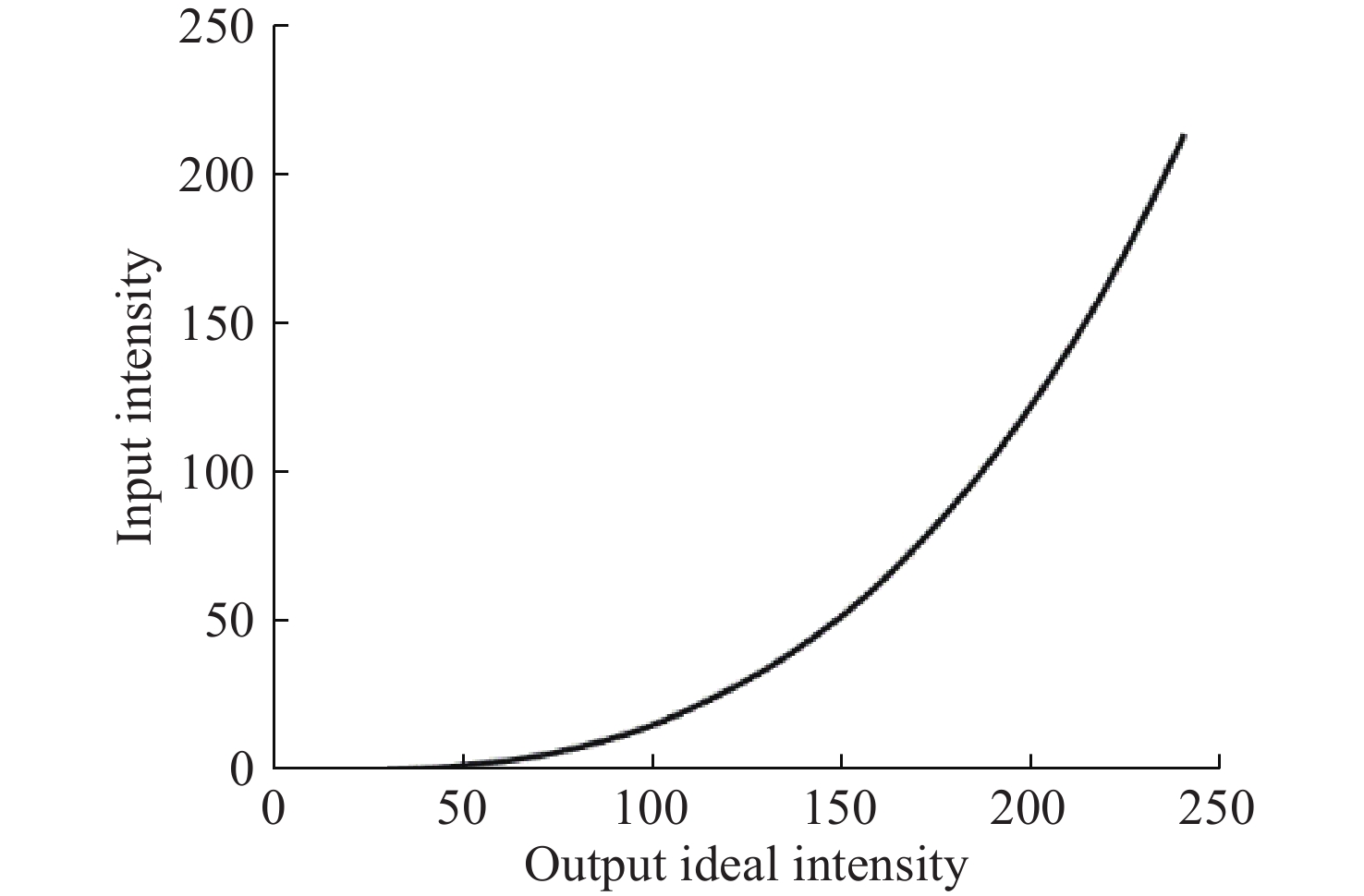
条纹投影技术在三维测量和表面形貌重建中得到广泛应用，其相位质量是决定测量精度的关键因素。然而，输入光强和输出光强之间的非线性效应是导致相位误差的主要来源之一。为了解决这一问题，本文提出了一种新的系统非线性主动校正方法。该方法首先通过对标准平面投影少量的均匀灰度图像，获取输入光强与输出光强的变化规律。然后，将这一规律与系统非线性主动校正结合，建立了基于输入输出光强变化的系统非线性模型。利用遗传算法求解最优编码值，从而通过条纹编码主动校正了投影条纹。校正后的条纹有效减少了非线性效应带来的影响，大幅提升了相位获取的质量。为了验证所提方法的有效性，以三步相移为例进行了计算机仿真。结果表明，标准误差降低了88%，最大误差减少了85.5%。在实际标准平面实验中，校正后标准相位误差由
0.0706 rad降至0.0168 rad，最大相位误差由0.4129 rad降至0.0960 rad。在人脸石膏模型实验中，校正后标准相位误差由0.0472 rad降至0.0102 rad，最大相位误差由0.2990 rad降至0.2408 rad。在复杂形貌人脸石膏件的三维重建中，校正后表面质量显著提升，影响相位质量的水波纹效应大幅减小。与现有的大步相移方法相比，本文提出的方法具有高质量的相位获取精度，而且在所需数据量和操作便捷性方面也具有明显优势，显示出广泛的应用前景。Abstract:Stripe projection technology is widely used in 3D measurement and surface morphology reconstruction, where phase quality is a critical determinant of measurement accuracy. However, the nonlinear relationship between input and output light intensity is a major source of phase error. To address this issue, this paper introduces a novel system nonlinear active correction method. This method captures the variation pattern between input and output light intensity by projecting a small number of uniform gray-scale images onto a standard plane. This pattern is then integrated with active system nonlinear correction to construct a system nonlinear model based on the input-output light intensity variation. Genetic algorithms are used to optimize the coding values, which are then used to actively correct the projected fringes via fringe coding. The corrected fringes effectively reduce the influence of nonlinear effects, thereby significantly improving the quality of phase acquisition. To validate the proposed method, computer simulations were performed using three-step phase shifting. The results showed an 88% reduction in the standard error and an 85.5% reduction in the maximum error. In actual standard plane experiments, the corrected standard phase error decreased from
0.0706 rad to0.0168 rad, and the maximum phase error decreased from0.4129 rad to0.0960 rad. In the face plaster model experiments, the corrected standard phase error decreased from0.0472 rad to0.0102 rad, and the maximum phase error decreased from0.2990 rad to0.2408 rad. In 3D reconstruction of complex morphology plaster models of human faces, the surface quality was significantly improved, and the water ripple effect, which affects the phase quality, was significantly reduced. Compared with existing large-step phase-shifting methods, the proposed method not only achieves high-quality phase acquisition accuracy, but also offers clear advantages in terms of required data volume and operational convenience, demonstrating broad application potential. -
图 3 输入光强与理想输出光强关系
Figure 3. Relationship between input light intensity and ideal output light intensity
图 5 仿真相移条纹图
Figure 5. Comparison of pre-correction and post-correction phases with the ideal unwrapped phase
图 10 牛皮纸板平面测量相位对比
Figure 10. Comparison of phase measurement for cowhide cardboard plane measurement
表 1 相位误差仿真模拟结果
Table 1. Simulation results of phase error
Method Uncorrected Corrected Std. phase error/rad 0.2894 0.036 Max phase error/rad 0.4120 0.060 
下载: 导出CSV
表 3 人脸石膏件实验相位误差结果
Table 3. Phase error results of facial gypsum piece experiment
Method Uncorrected Others Ours Std. phase error/rad 0.0472 0.0164 0.0102 Max phase error/rad 0.2990 0.2561 0.2408
下载: 导出CSV
表 2 标准平面实验相位误差结果
Table 2. Phase error results from standard plane experiments
Method Uncorrected Others Ours Std. phase error/rad 0.0706 0.0227 0.0168 Max phase error/rad 0.4129 0.1320 0.0960
下载: 导出CSV
-
[1] 刘泽隆, 李茂月, 卢新元, 等. 高动态范围条纹结构光在机检测技术及应用进展[J]. 中国光学(中英文),2024,17(1):1-18. doi: 10.37188/CO.2023-0068LIU Z L, LI M Y, LU X Y, et al. On-machine detection technology and application progress of high dynamic range fringe structured light[J]. Chinese Optics, 2024, 17(1): 1-18. (in Chinese). doi: 10.37188/CO.2023-0068 [2] 吕虹毓, 李茂月, 蔡东辰, 等. 光栅投影在机三维形貌检测技术研究进展[J]. 中国光学(中英文),2023,16(3):500-513. doi: 10.37188/CO.2022-0083LV H Y, LI M Y, CAI D CH, et al. Research progress of grating projection on machine 3D topography inspection technology[J]. Chinese Optics, 2023, 16(3): 500-513. (in Chinese). doi: 10.37188/CO.2022-0083 [3] 张宗华, 李雁玲, 高峰, 等. 面向结构光三维测量的相位展开技术综述(特邀)[J]. 红外与金宝搏188软件怎么用 工程,2023,52(8):20230126. doi: 10.3788/IRLA20230126ZHANG Z H, LI Y L, GAO F, et al. Phase unwrapping technology for structured light three-dimensional measurement: a review (invited)[J]. Infrared and Laser Engineering, 2023, 52(8): 20230126. (in Chinese). doi: 10.3788/IRLA20230126 [4] 王鹏, 刘佳琪, 孙长库, 等. 正交条纹级次分区域预编码校正Gamma非线性方法[J]. 红外与金宝搏188软件怎么用 工程,2022,51(6):20210503. doi: 10.3788/IRLA20210503WANG P, LIU J Q, SUN CH K, et al. Correction of Gamma nonlinearity method by orthogonal fringe order subregional precoding[J]. Infrared and Laser Engineering, 2022, 51(6): 20210503. (in Chinese). doi: 10.3788/IRLA20210503 [5] HOANG T, PAN B, NGUYEN D, et al. Generic gamma correction for accuracy enhancement in fringe-projection profilometry[J]. Optics Letters, 2010, 35(12): 1992-1994. doi: 10.1364/OL.35.001992 [6] ZHANG S. Comparative study on passive and active projector nonlinear gamma calibration[J]. Applied Optics, 2015, 54(13): 3834-3841. doi: 10.1364/AO.54.003834 [7] ZHU ZH M, XU X K, LONG W Q, et al. The optimal algorithm for eliminating nonlinear error in phase measurement profilometry based on global statistical phase feature function[J]. Measurement Science and Technology, 2024, 35(6): 065020. doi: 10.1088/1361-6501/ad34ee [8] 王子龙, 徐洪志, 杨玲玲, 等. 基于1/6周期查找表的相移条纹非线性误差补偿法[J]. 光学学报,2024,44(9):0912002. doi: 10.3788/AOS231999WANG Z L, XU H ZH, YANG L L, et al. Nonlinear error compensation method for phase-shifted fringe using 1/6-period lookup table[J]. Acta Optica Sinica, 2024, 44(9): 0912002. (in Chinese). doi: 10.3788/AOS231999 [9] XIONG CH, YAO J, CHEN J B, et al. A convenient look-up-table based method for the compensation of non-linear error in digital fringe projection[J]. Theoretical and Applied Mechanics Letters, 2016, 6(1): 49-53. doi: 10.1016/j.taml.2015.12.005 [10] 李茂月, 蔡东辰, 赵伟翔, 等. 航空叶片形貌高精度结构光扫描视点规划[J]. 中国光学(中英文),2023,16(4):802-815. doi: 10.37188/CO.2022-0221LI M Y, CAI D CH, ZHAO W X, et al. High precision structural light scanning viewpoint planning for aircraft blade morphology[J]. Chinese Optics, 2023, 16(4): 802-815. (in Chinese). doi: 10.37188/CO.2022-0221 [11] KATOCH S, CHAUHAN S S, Kumar V. A review on genetic algorithm: past, present, and future[J]. Multimedia Tools and Applications, 2021, 80(5): 8091-8126. doi: 10.1007/s11042-020-10139-6 [12] NIKIFOROV D, EFIMOV S, PROVORNYKH I. Studying how the configuration of a genetic algorithm affects the solution of a problem[C]. Proceedings of 2024 International Russian Smart Industry Conference, IEEE, 2024: 768-772. [13] LIU Y K, YU X, XUE J P, et al. A flexible phase error compensation method based on probability distribution functions in phase measuring profilometry[J]. Optics & Laser Technology, 2020, 129: 106267. [14] WANG Y W, ZHU H J, CAI J X, et al. Intensity-averaged double three-step phase-shifting algorithm with color-encoded fringe projection[J]. Photonics, 2022, 9(3): 173. doi: 10.3390/photonics9030173 [15] KAMAGARA A, WANG X ZH, LI S K. Towards gamma-effect elimination in phase measurement profilometry[J]. Optik, 2018, 172: 1089-1099. doi: 10.1016/j.ijleo.2018.07.059 [16] MUÑOZ A, FLORES J L, PARRA-ESCAMILLA G, et al. Least-squares gamma estimation in fringe projection profilometry[J]. Applied Optics, 2021, 60(5): 1137-1142. doi: 10.1364/AO.415056 -
下载:
计量
- 文章访问数: 43
- HTML全文浏览量: 29
- PDF下载量: 0
- 被引次数: 0
