二维线性调频<i>Z</i>变换用于光束质量<i>β</i>因子计算 -

姓名
邮箱
手机号码
标题
留言内容
验证码

二维线性调频Z变换用于光束质量β因子计算

doi:10.37188/CO.2020-0079

中国工程物理研究院计量测试中心，四川绵阳 621900

基金项目:国防科工局技术基础项目（No. JSJL201712B002）

详细信息

作者简介:
王艳茹(1983—)，女，陕西渭南人，博士研究生，高级工程师，2011年于中国科学院光电技术研究所获得博士学位，目前主要从事光学计量与检测技术方面的研究工作。E-mail:wyr3235@163.com

中图分类号:O438
计量
- 文章访问数:1900
- HTML全文浏览量:410
- PDF下载量:79
- 被引次数:0
出版历程
- 收稿日期:2020-04-27
- 修回日期:2020-05-29
- 网络出版日期:2020-09-16
- 刊出日期:2020-10-01

Beam qualityβfactor calculation based on two-dimensional chirpZtransformation

Metrology and Testing Center, China Academy of Engineering Physics, MianYang 621900, China

Funds:Supported by Basic Technology Project of Science Technology and Industry for National Defense (No. JSJL201712B002)

More Information

Corresponding author:wyr3235@163.com

摘要

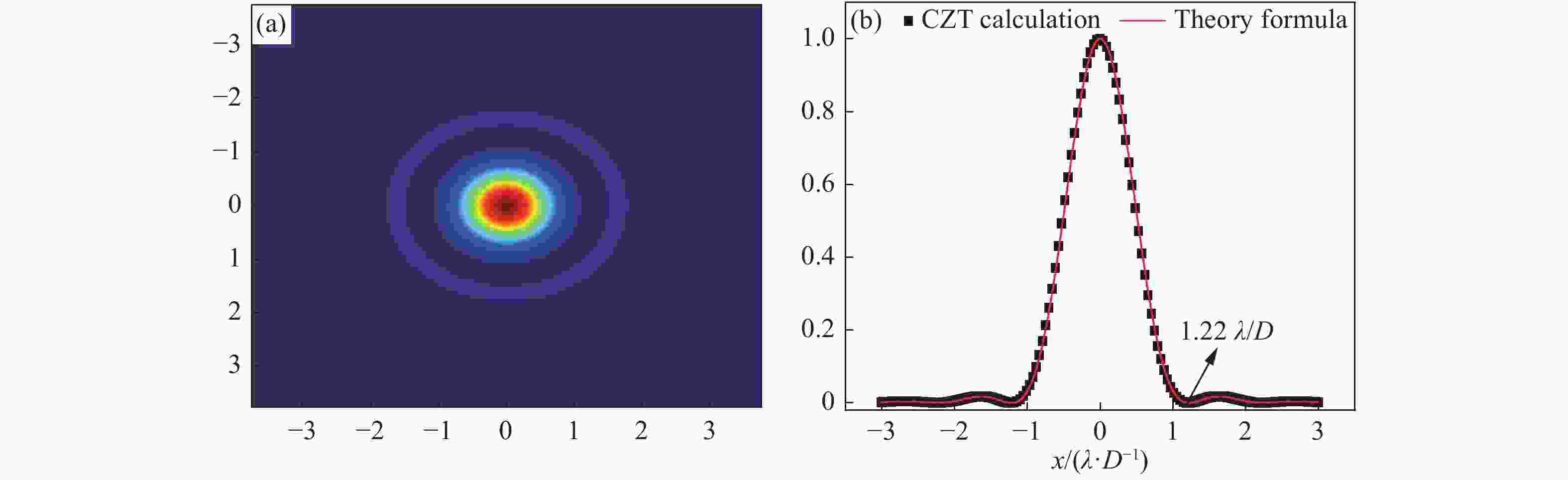
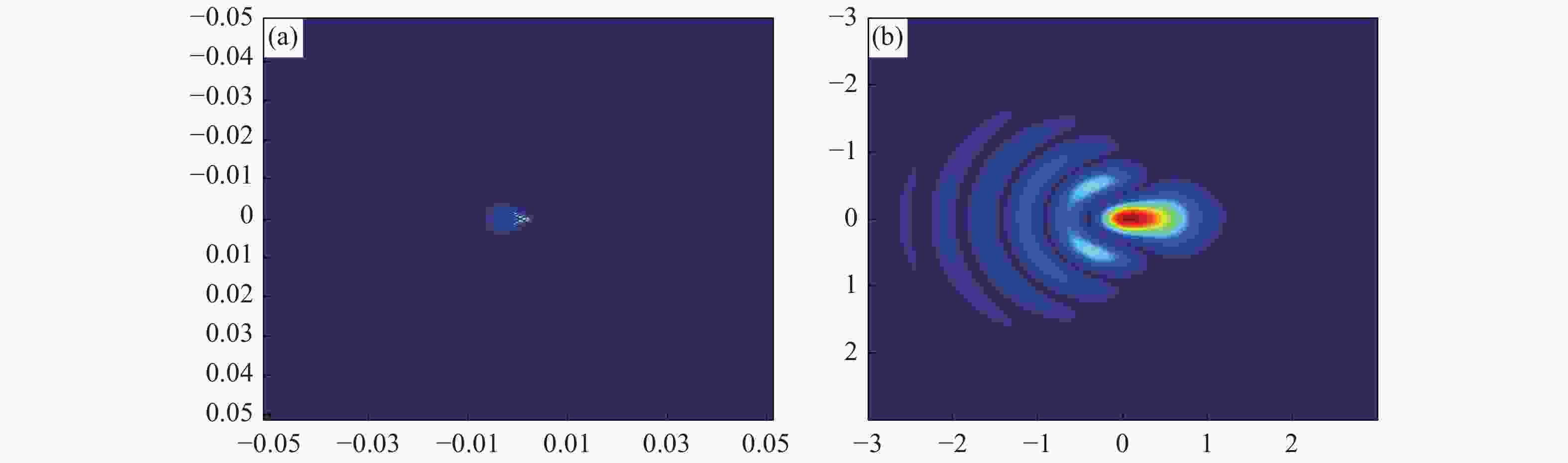
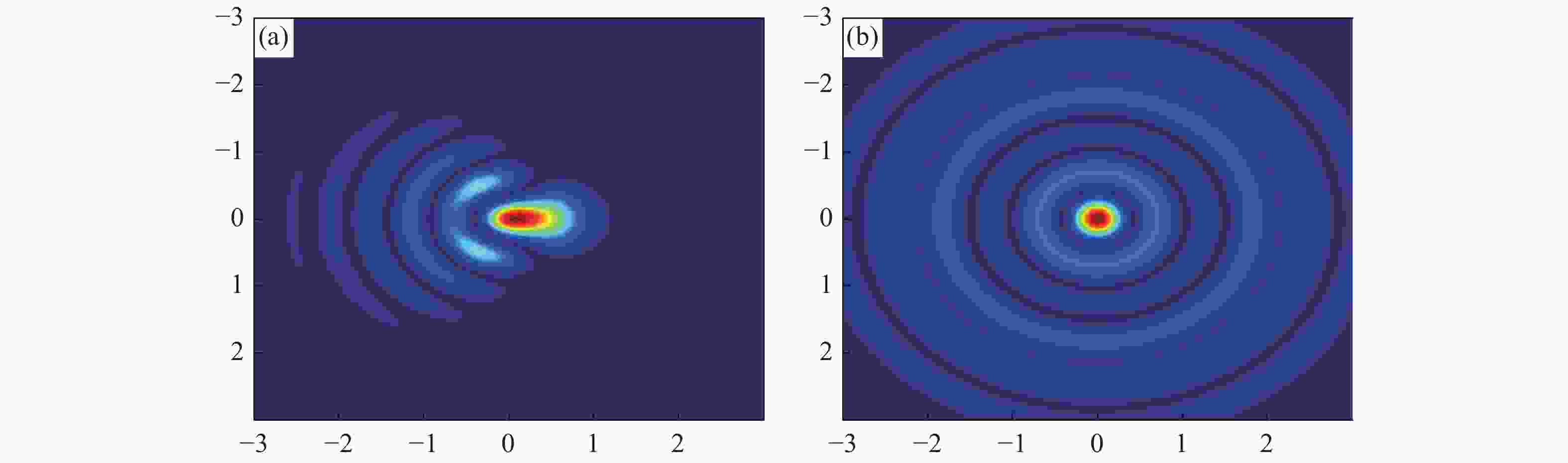
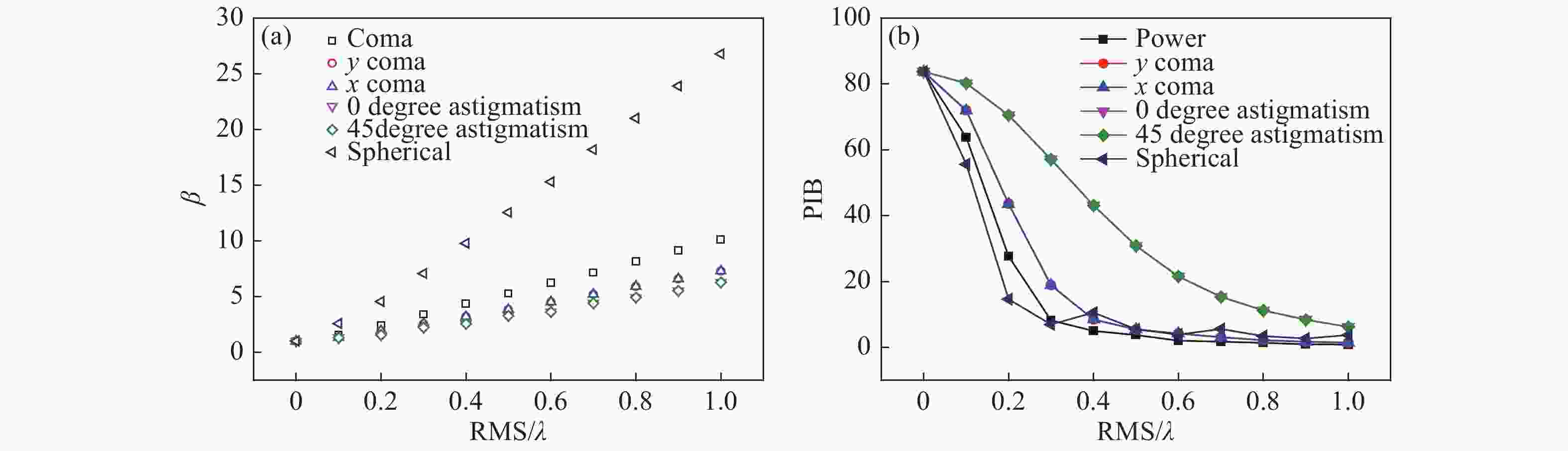
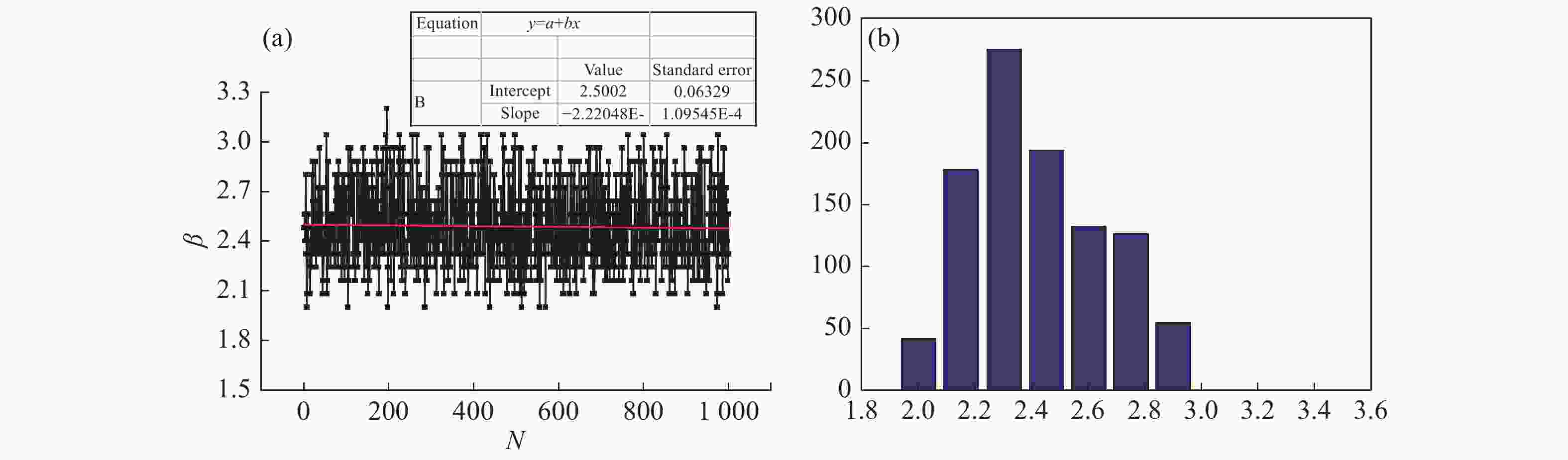
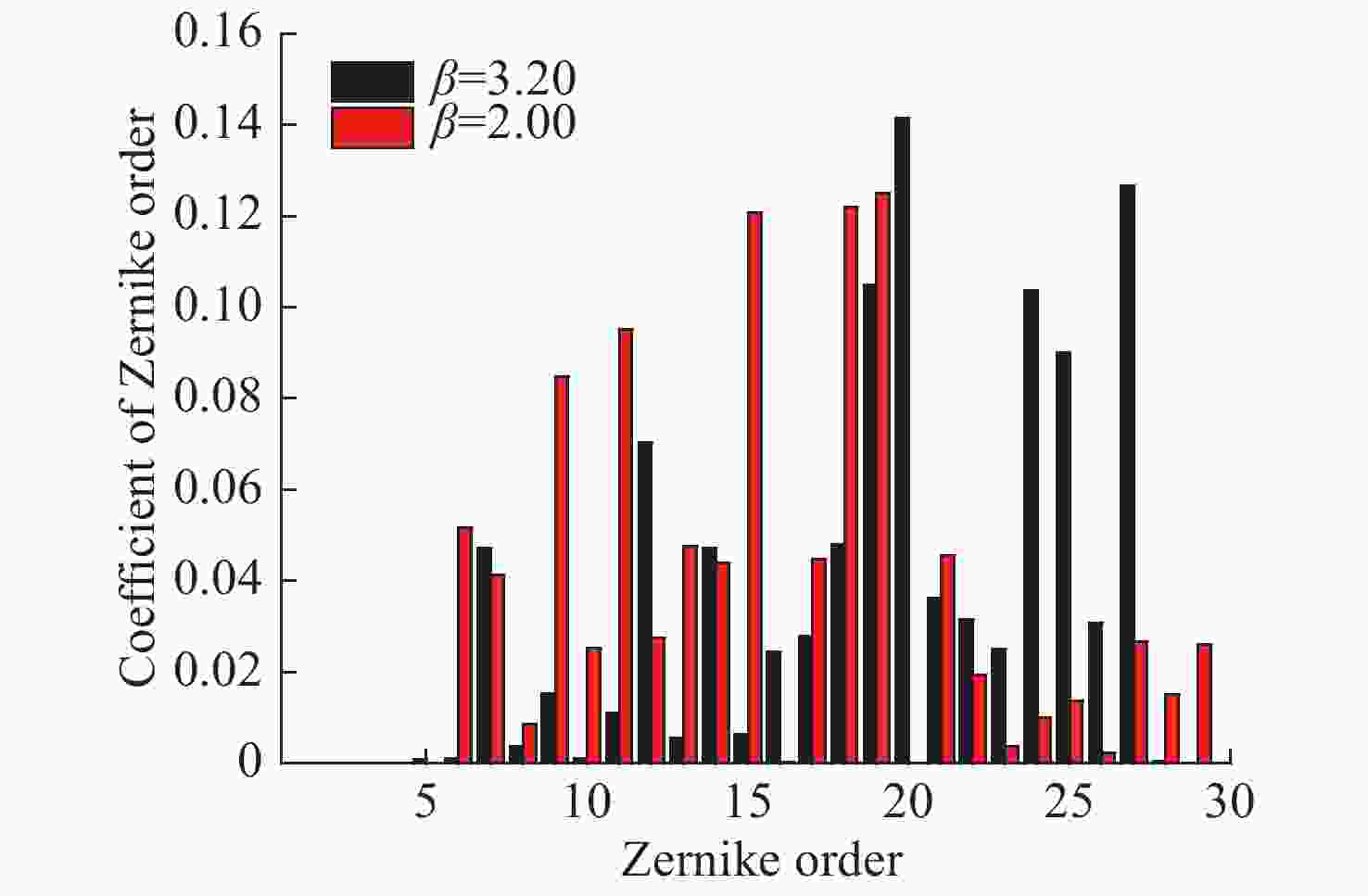
摘要:本文提出了一种基于二维线性调频 Z变换的衍射光场分布快速计算方法，该方法在不增加运算量的情况下可以显著提高光场分布的图像分辨率，进而能够得到更准确的光束质量 β因子值。在算法正确性验证的基础上，本文数值模拟了不同光束波前畸变的均方根RMS值与光束质量 β因子的对应关系。仿真结果表明，在像差分布RMS值相同的前提下，几种低阶像差类型中球差类型的像差对光束质量的影响最大。为了模拟不同光斑分布形态，随机Zernike像差组合方式的光束质量 β因子的仿真计算结果表明：相同的RMS值情况下，高阶像差占比较高的像差组合方式对应的光束质量 β因子较大。
- 数值模拟/
- 波前像差/
- 光束质量/
- 线性调频Z变换
Abstract:An algorithm for fast calculation of the field distribution of diffraction based on two-dimension chirp Ztransformation is proposed. The proposed algorithm does not increase computation and significantly improves the resolution of the diffraction distribution and obtains a more accurate beam quality βfactor. After verifying the correctness of the proposed algorithm, the corresponding relationship between the RMS (Root-Mean-Square) of the beam′s wavefront aberration and βfactor is simulated. The simulation results show that with the same RMS value, the effect of a spherical aberration on the βfactor is the strongest among the lower order Zernike aberrations. In order to simulate the different distribution of beam spots, the βfactors are calculated based on different random Zernike wavefront aberrations. The results indicate that a larger proportion of high-order Zernike aberrations in the cumulative aberrations induces a bigger βfactor with an identical RMS value.
- numerical simulation/
- wavefront aberration/
- beam quality/
- chirpZtransformation

HTML全文

图 1二维Z变换算法流程图

Figure 1.Flowchart of two-dimensional chirpZtransformation (CZT)

下载: 全尺寸图片幻灯片

图 2（a）线性调频Z变换的计算路径和（b）透光孔函数

Figure 2.(a) The calculation path of CZT algorithm and (b) transparent hole function used in the calculation

下载: 全尺寸图片幻灯片

图 3（a）探测面上的衍射光强分布及（b）衍射强度曲线

Figure 3.(a) Diffraction intensity distribution at the detection plane and (b) diffraction intensity curve in one dimension

下载: 全尺寸图片幻灯片

图 4（a）s-fft算法及（b）CZT算法的衍射强度分布

Figure 4.Diffraction distributions of (a) s-fft algorithm and (b) CZT algorithm

下载: 全尺寸图片幻灯片

图 5（a）彗差和（b）球差对应的探测面上的衍射强度分布

Figure 5.Diffraction distributions of (a) coma wavefront aberration and (b) spherical wavefront aberration

下载: 全尺寸图片幻灯片

图 6（a）光束质量β因子和（b）桶中功率PIB随波像差RMS值的变化关系

Figure 6.（a）Beam qualityβfactor and (b) PIB changing with RMS of wavefront aberration

下载: 全尺寸图片幻灯片

图 7随机像差对应的光束质量β因子波动（a）和β因子的统计分布（b）

Figure 7.（a）Fluctuation ofβfactor with random wavefront aberrations and (b) statistical distribution of theβfactor

下载: 全尺寸图片幻灯片

图 8Zernike多项式系数分布图

Figure 8.Coefficient ofZernike polynomial

下载: 全尺寸图片幻灯片

图 9不同均方根RMS值的随机像差对应的β因子变化情况

Figure 9.Variation in theβfactor corresponding to random wavefront aberrations for different RMS values

下载: 全尺寸图片幻灯片

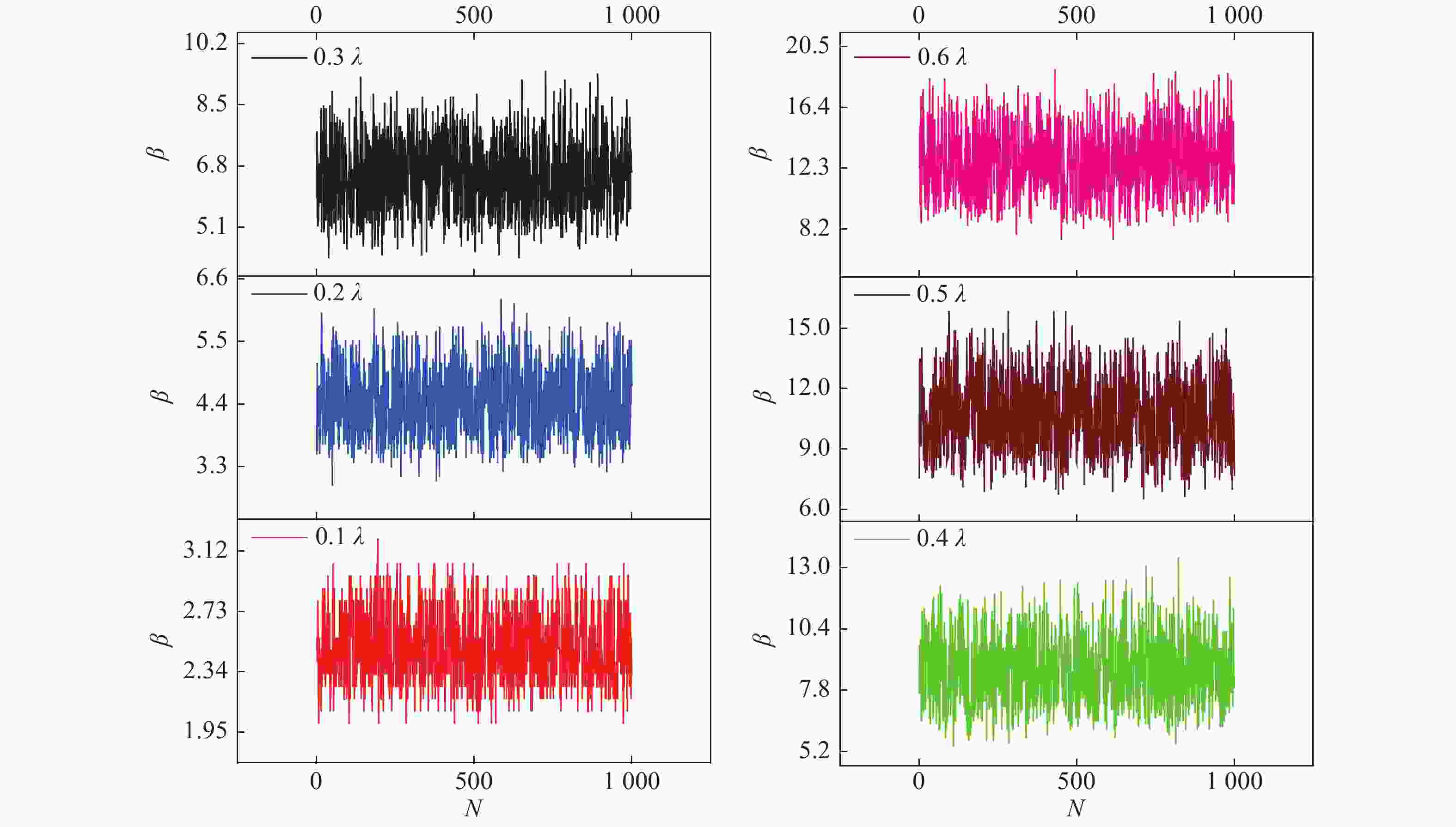
表 1光束质量β因子统计结果

Table 1.Statistical results of theβfactor

波像差RMS值	β因子统计均值	β因子标准偏差
0.1λ	2.50	0.06
0.2λ	4.42	0.04
0.3λ	6.56	0.07
0.4λ	8.66	0.10
0.5λ	10.81	0.13
0.6λ	12.64	0.16
0.7λ	14.87	0.18
0.8λ	17.11	0.21
0.9λ	18.67	0.22
1.0λ	20.90	0.24

下载: 导出CSV

参考文献 (17)

吕百达, 康小平. 对光束质量一些问题的认识[J]. 红外与工程,2007,36(1):47-51.doi:10.3969/j.issn.1007-2276.2007.01.012

LÜ B D, KANG X P. Some aspects of laser beam quality[J].Infrared and Laser Engineering, 2007, 36(1): 47-51. (in Chinese)doi:10.3969/j.issn.1007-2276.2007.01.012

田英华, 叶一东, 向汝建, 等. 光束质量因子测量的不确定度分析[J]. 强与粒子束,2008,20(7):1076-1078.

TIAN Y H, YE Y D, XIANG R J,et al. Evaluation of uncertainty in beam quality measurement[J].High Power Laser and Particle Beams, 2008, 20(7): 1076-1078. (in Chinese)

王云萍, 黄建余, 乔广林. 高能光束质量的评价方法[J]. 光电子· ,2001,12(10):1029-1033.doi:10.3321/j.issn:1005-0086.2001.10.012

WANG Y P, HUANG J Y, QIAO G L. A method for evaluating high energy laser beam quality[J].Journal of Optoelectronics·Laser, 2001, 12(10): 1029-1033. (in Chinese)doi:10.3321/j.issn:1005-0086.2001.10.012

闫宏宇, 高欣, 宋健, 等. 976 nm宽条形高功率半导体器的光束质量M²评价[J]. 发光学报,2019,40(2):196-203.doi:10.3788/fgxb20194002.0196

YAN H Y, GAO X, SONG J,et al. Evaluation of beam qualityM²for 976 nm wide stripe high power semiconductor laser[J].Chinese Journal of Luminescence, 2019, 40(2): 196-203. (in Chinese)doi:10.3788/fgxb20194002.0196

陈诚, 郑加金, 韦玮, 等. 基于CCD测量光束质量M²[J]. 发光学报,2017,38(5):642-647.doi:10.3788/fgxb20173805.0642

CHEN CH, ZHENG J J, WEI W,et al. Measurement of laser beam qualityM²based on CCD[J].Chinese Journal of Luminescence, 2017, 38(5): 642-647. (in Chinese)doi:10.3788/fgxb20173805.0642

许坤, 付林杰, 钟发成, 等. 高光束质量垂直腔面发射器同相耦合阵列[J]. 发光学报,2018,39(6):844-849.doi:10.3788/fgxb20183906.0844

XU K, FU L J, ZHONG F CH,et al. High beam quality in-phase coupled vertical cavity surface emitting laser array[J].Chinese Journal of Luminescence, 2018, 39(6): 844-849. (in Chinese)doi:10.3788/fgxb20183906.0844

鲜浩, 姜文汉. 波像差与光束质量指标的关系[J]. 中国 ,1999,26(5):415-419.doi:10.3321/j.issn:0258-7025.1999.05.007

XIAN H, JIANG W H. The relation between wavefront aberration and the beam quality factor[J].Chinese Journal of Lasers, 1999, 26(5): 415-419. (in Chinese)doi:10.3321/j.issn:0258-7025.1999.05.007

李新阳, 鲜浩, 王春鸿, 等. 波像差与光束质量β因子的关系[J]. 中国 ,2005,32(6):798-802.doi:10.3321/j.issn:0258-7025.2005.06.016

LI X Y, XIAN H, WANG CH H,et al. Relationship between beam quality factorβand wavefront error[J].Chinese Journal of Lasers, 2005, 32(6): 798-802. (in Chinese)doi:10.3321/j.issn:0258-7025.2005.06.016

李新阳, 姜文汉, 王春红, 等. 湍流大气中哈特曼传感器的模式波前复原误差[J]. 强与粒子束,2000,12(2):148-154.

LI X Y, JIANG W H, WANG CH H,et al. Modal reconstruction error of the hartmann sensor on measuring the atmosphere disturbed wavefront[J].High Power Laser and Particle Beams, 2000, 12(2): 148-154. (in Chinese)

李新阳, 姜文汉, 王春红, 等. 湍流大气中哈特曼传感器的模式波前复原误差II[J]. 强与粒子束,2000,12(3):319-323.

LI X Y, JIANG W H, WANG CH H,et al. Modal reconstruction error of the hartmann sensor on measuring the atmosphere disturbed wavefront II[J].High Power Laser&Particle Beams, 2000, 12(3): 319-323. (in Chinese)

李新阳, 姜文汉. 哈特曼传感器对湍流畸变波前的泽尼克模式复原误差[J]. 强与粒子束,2002,14(2):243-249.

LI X Y, JIANG W H. Zernike modal wavefront reconstruction error of Hartmann sensor on measuring the atmosphere disturbed wavefront[J].High Power Laser and Particle Beams, 2002, 14(2): 243-249. (in Chinese)

刘志强, 宋庆和, 刘超, 等. 基于虚拟光波场的菲涅耳衍射计算及应用研究[J]. 应用光学,2018,39(2):196-199.

LIU ZH Q, SONG Q H, LIU CH,et al. Fresnel diffraction calculation with virtual light wave field and its application[J].Journal of Applied Optics, 2018, 39(2): 196-199. (in Chinese)

胡琪, 王喆, 刘洪顺, 等. 基于单次傅里叶变换的分段衍射算法[J]. 中国光学,2018,11(4):568-575.doi:10.3788/co.20181104.0568

HU Q, WANG ZH, LIU H SH,et al. Step diffraction algorithm based on single fast fourier transform algorithm[J].Chinese Optics, 2018, 11(4): 568-575. (in Chinese)doi:10.3788/co.20181104.0568

向红丽, 范琦, 李云, 等. FFT计算菲涅尔衍射相位的跳变与矫正研究[J]. 计算机与现代化,2018(8):35-38, 50.doi:10.3969/j.issn.1006-2475.2018.08.007

XIANG H L, FAN Q, LI Y,et al. Jump and correction of Fresnel diffraction phase[J].Computer and Modernization, 2018(8): 35-38, 50. (in Chinese)doi:10.3969/j.issn.1006-2475.2018.08.007

钱克矛, 李川奇. 频谱校正的线性调频Z变换方法[J]. 振动工程学报,2000,13(4):628-632.doi:10.3969/j.issn.1004-4523.2000.04.019

QIAN K M, LI CH Q. New spectrum correction method based on chirp Z transform[J].Journal of Vibration Engineering, 2000, 13(4): 628-632. (in Chinese)doi:10.3969/j.issn.1004-4523.2000.04.019

徐建军, 胡光东, 李锦明. 线性调频Z变换在信号频谱分析中的应用[J]. 应用基础与工程科学学报,2009,17(6):966-972.doi:10.3969/j.issn.1005-0930.2009.06.019

XU J J, HU G D, LI J M. Chirp-Z transform and its applications in spectrum analysis[J].Journal of Basic Science and Engineering, 2009, 17(6): 966-972. (in Chinese)doi:10.3969/j.issn.1005-0930.2009.06.019

赖俊森, 杨爱英, 孙雨南. 线性调频Z变换在光采样光性能监测中的应用[J]. 北京理工大学学报,2011,31(7):833-837, 854.

LAI J S, YANG A Y, SUN Y N. Application of Chirp-Z transform to the optical-sampling optical performance monitoring[J].Transactions of Beijing Institute of Technology, 2011, 31(7): 833-837, 854. (in Chinese)

施引文献

附加信息 (0)

访问统计