The poynting vector and angular momentum density of Cosh-Pearcey-Gaussian vortex beams in uniaxial crystals
doi: 10.37188/CO.EN.2022-0007
-
摘要:
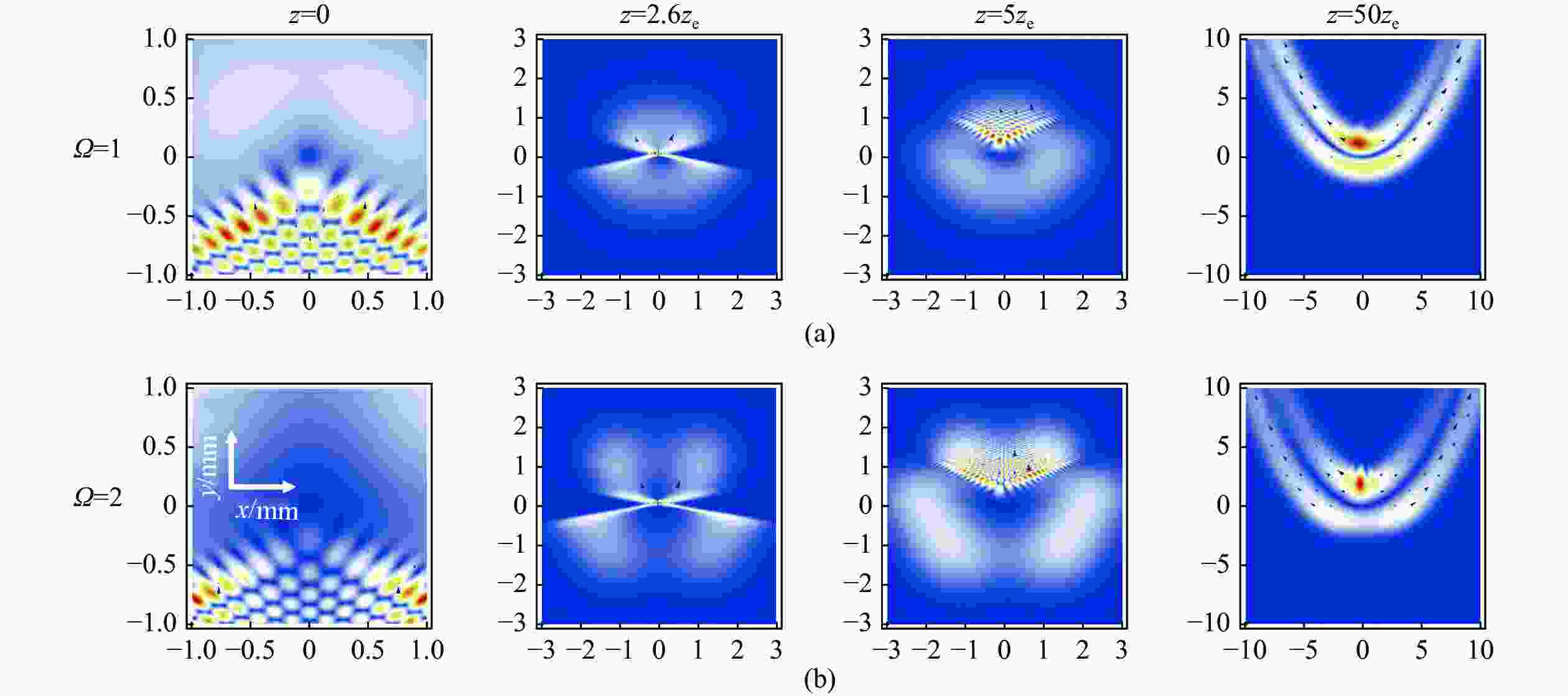
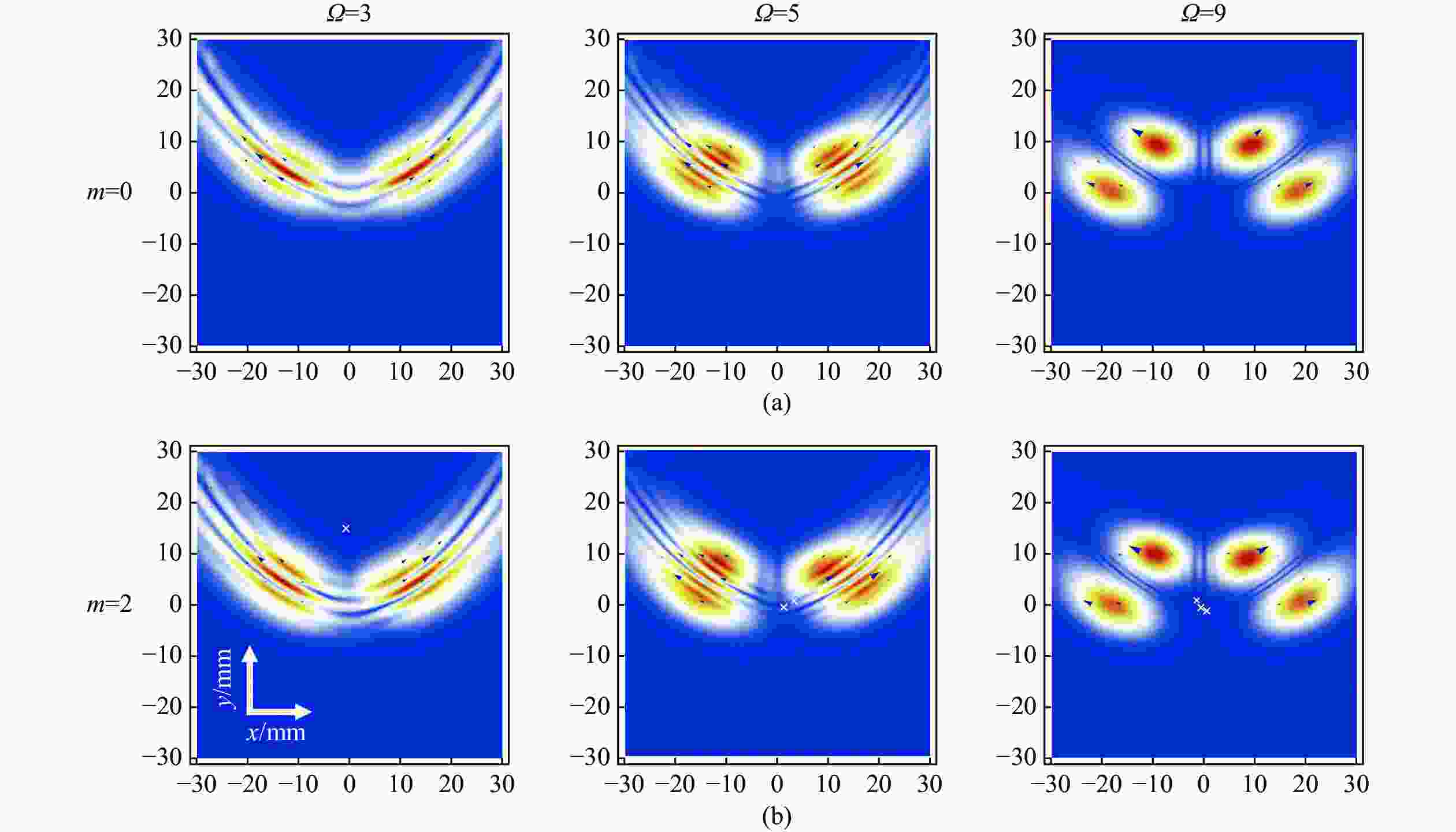
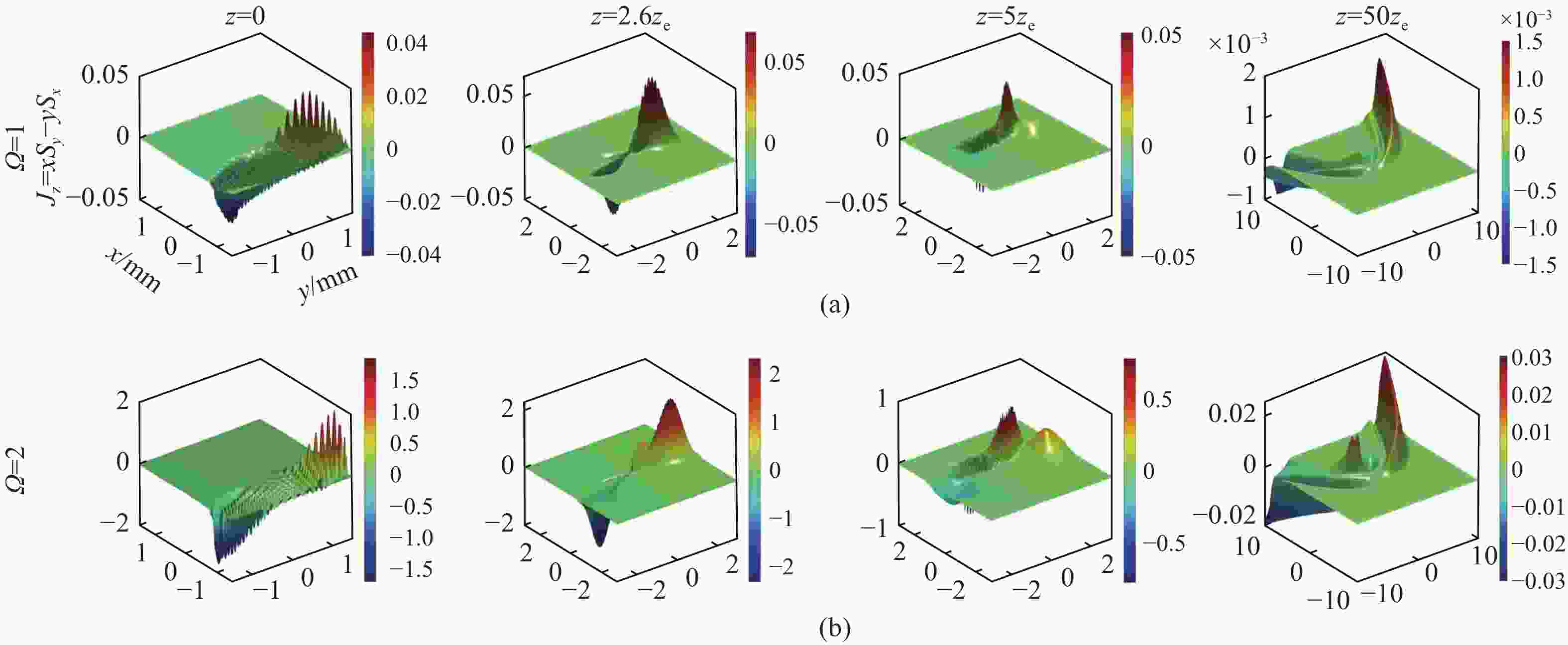
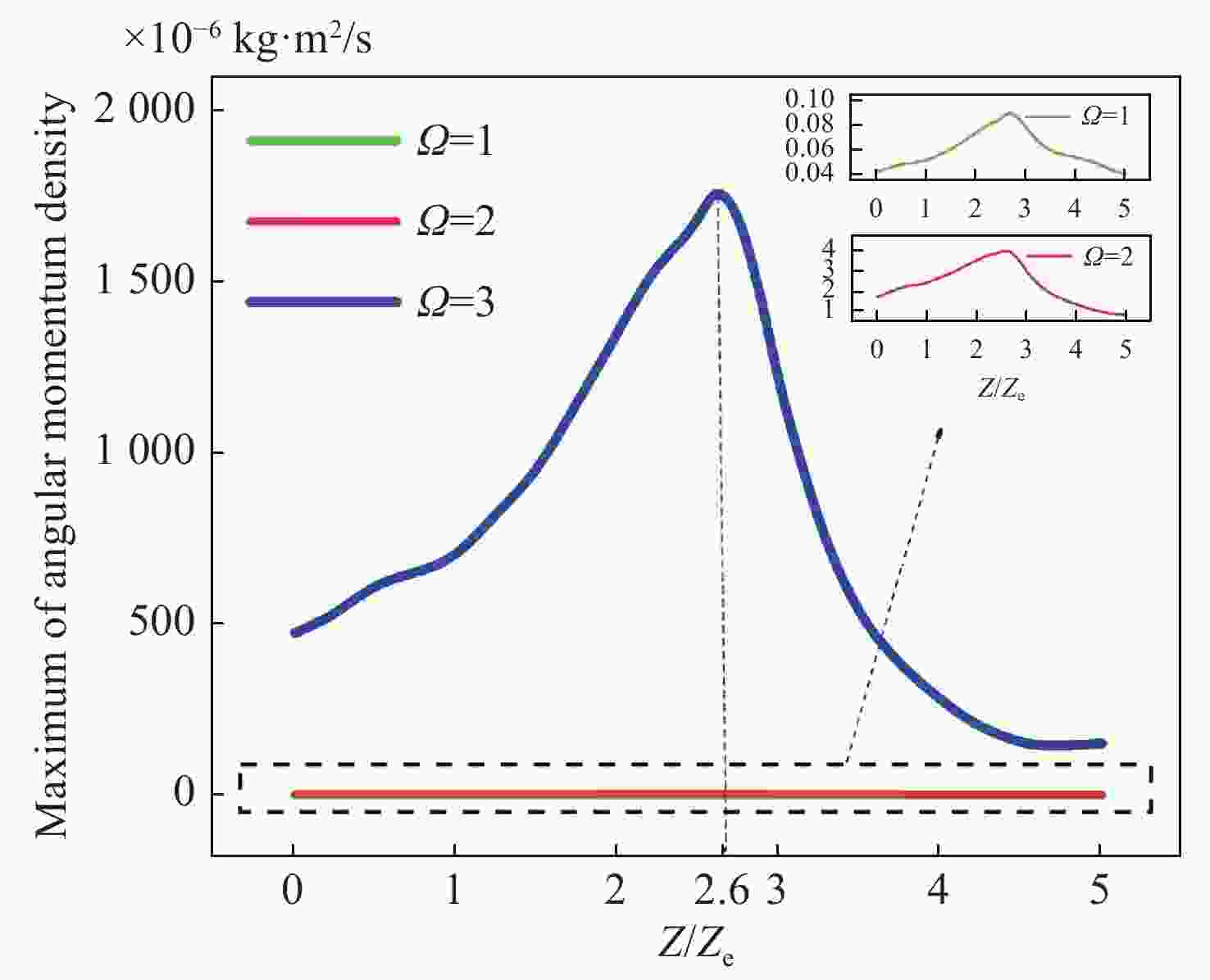
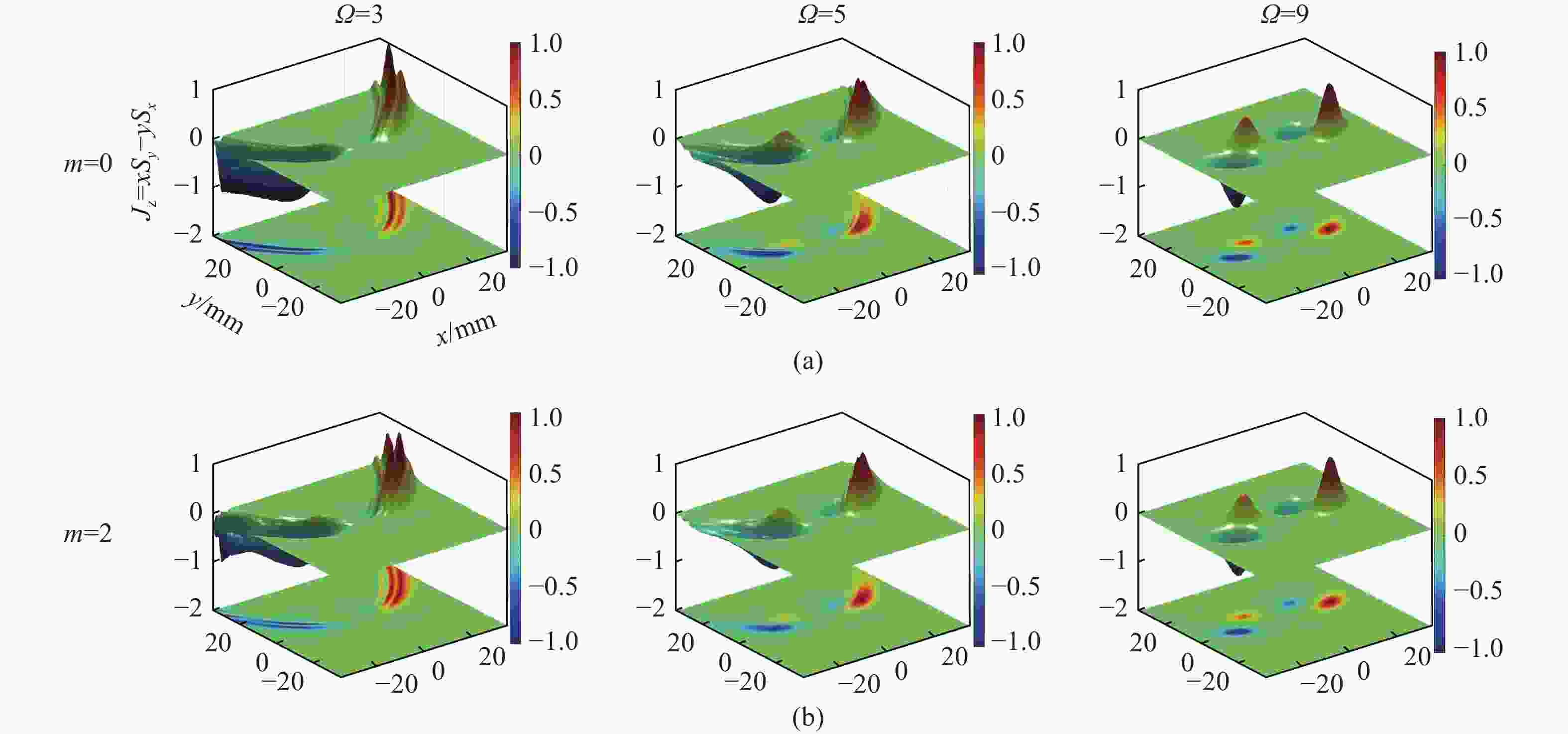
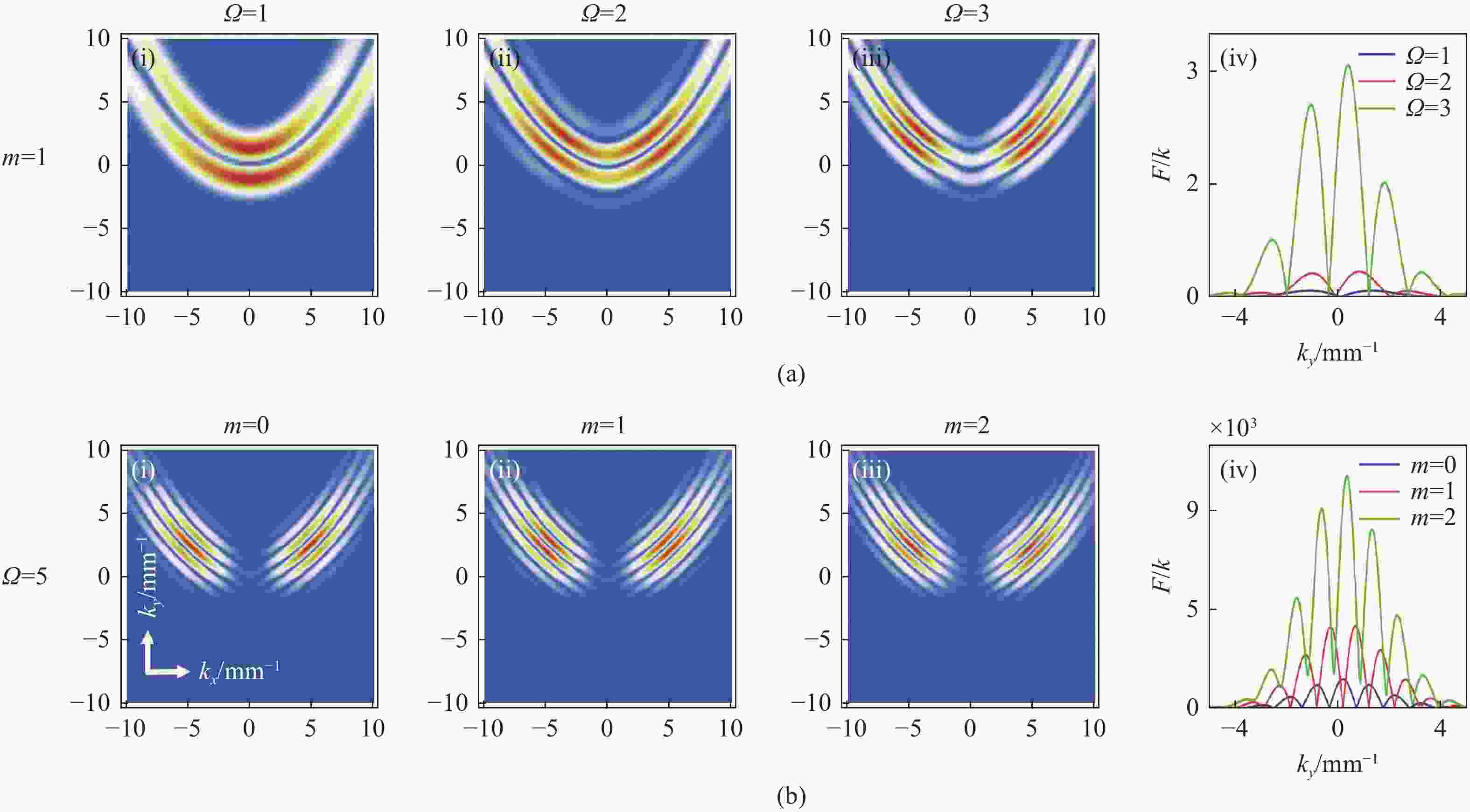
为了分析和研究Cosh-Pearcey-Gaussian涡旋 (CPeGV)光束的传播特性，通过皮尔斯积分式得到了CPeGV光束传播的一般表达式，推导出CPeGV光束在单轴晶体中传播的解析式。详细研究了CPeGV光束在单轴晶体中传播时的纵向和横向坡印廷矢量和角动量密度(AMD)。探讨了双曲余弦参数、拓扑电荷和传播距离对CPeGV光束传播特性的影响。研究结果表明：与PeG光束相比，CPeGV光束的调制自由度更高。较大的双曲余弦调制参数可以控制能量沿横向坡印廷矢量方向传递，从而不仅可以改变能量分布也可以使AMD峰值变大。在远场，CPeGV光束的纵向坡印廷矢量随着双曲余弦参数的增大会从抛物线形状分离为四个波瓣的分布形状。而拓扑电荷会影响远场抛物线形状中暗区的数量。本文研究将有助于更好地理解 CPeGV光束在单轴晶体中的传播特性，并有助于信息传输和存储的应用。
-
关键词:
- Cosh-Pearcey-Gaussian涡旋光束 /
- 坡印廷矢量 /
- 角动量密度 /
- 单轴晶体
Abstract:We investigate a family of Cosh-Pearcey-Gaussian Vortex (CPeGV) beams, obtain the general propagation expressions of a CPeGV beam, and study the longitudinal and transverse Poynting vector and Angular Momentum Density (AMD) when the CPeGV beams propagate in uniaxial crystals. The effects of the cosh modulation parameter, topological charge, and propagation distance on the propagation properties of CPeGV beams are discussed. A larger cosh modulation parameter can lead the energy transfer significantly along the transverse Poynting vector direction. Moreover, we also investigate how the cosh modulation parameter and topological charge influence the propagation properties in the far-field. A larger cosh modulation parameter can lead AMD to present four-lobe structures rather than their usual parabolic curve. Our investigation will provide a better understanding of the state of the CPeGV beams propagating in uniaxial crystals and be useful for applications in information transmission.
-
Figure 1. The dependence of Fourier spectrum of CPeGV beams on cosh modulation parameter Ω and topological charge m; (a) the topological charge m= 1; (b) the cosh modulation parameter Ω=5.
Figure 2. The intensity (backgrounds) and the transverse Poynting vector (arrows) of the CPeGV beams propagating in uniaxial crystal for different propagation distances z with different cosh modulation parameters Ω and ne=1.2no; (a): Ω=1; (b): Ω=2 and m=1.
Figure 3. The longitudinal and transverse Poynting vectors of the CPeGV beams for different cosh modulation parameters Ω and topological charges m at z=300ze. (a): m=0; (b): m=2.
Figure 4. The longitudinal AMD of the CPeGV beams propagating in uniaxial crystal for different propagation distances z with different cosh modulation parameters Ω and ne=1.2no, m=1. (a): Ω=1; (b): Ω=2
Figure 5. Maximum of angular momentum density of CPeGV beams in uniaxial crystal for different propagation distances z with different cosh modulation parameters Ω
Figure 6. The normalized AMD of the CPeGV beams in uniaxial crystal at z=300ze for different cosh modulation parameters Ω with different topological charges and ne=1.2no; (a): m=0; (b): m=2
-
[1] PEARCEY T. XXXI. The structure of an electromagnetic field in the neighbourhood of a cusp of a caustic[J]. The London,Edinburgh,and Dublin Philosophical Magazine and Journal of Science, 1946, 37(268): 311-317. doi: 10.1080/14786444608561335 [2] RING J D, LINDBERG J, MOURKA A, et al. Auto-focusing and self-healing of Pearcey beams[J]. Optics Express, 2012, 20(17): 18955-18966. doi: 10.1364/OE.20.018955 [3] ZENG Z SH, DENG D M. Paraxial propagation of Pearcey Gaussian beams with the astigmatic phase in the chiral medium[J]. Journal of the Optical Society of America B, 2020, 37(1): 30-37. doi: 10.1364/JOSAB.37.000030 [4] HUANG ZH C, WU Y, LIN Z J, et al. Effects of the multi-order and off-axis vortex on the propagation of Pearcey Gaussian vortex beams with the astigmatic phase in a chiral medium[J]. Waves in Random and Complex Media, 2021: 1-11. [5] JIANG J J, MO ZH W, XU D L, et al. Elliptical Pearcey beam[J]. Optics Communications, 2022, 504: 127475. doi: 10.1016/j.optcom.2021.127475 [6] WU Y, ZHAO J J, LIN Z J, et al. Symmetric Pearcey Gaussian beams[J]. Optics Letters, 2021, 46(10): 2461-2464. doi: 10.1364/OL.425889 [7] LIU Y J, XU CH J, LIN Z J, et al. Auto-focusing and self-healing of symmetric odd-Pearcey Gauss beams[J]. Optics Letters, 2020, 45(11): 2957-2960. doi: 10.1364/OL.394443 [8] CIATTONI A, CINCOTTI G, PALMA C. Propagation of cylindrically symmetric fields in uniaxial crystals[J]. Journal of the Optical Society of America A, 2002, 19(4): 792-796. doi: 10.1364/JOSAA.19.000792 [9] CIATTONI A, PALMA C. Optical propagation in uniaxial crystals orthogonal to the optical axis: paraxial theory and beyond[J]. Journal of the Optical Society of America A, 2003, 20(11): 2163-2171. doi: 10.1364/JOSAA.20.002163 [10] ZHOU M L, CHEN CH D, CHEN B, et al. Propagation of an Airy-Gaussian beam in uniaxial crystals[J]. Chinese Physics B, 2015, 24(12): 124102. doi: 10.1088/1674-1056/24/12/124102 [11] DENG D M, CHEN CH D, ZHAO X, et al. Propagation of an Airy vortex beam in uniaxial crystals[J]. Applied Physics B, 2013, 110(3): 433-436. doi: 10.1007/s00340-012-5273-5 [12] XU CH J, LIN L D, HUANG ZH ZH, et al. Propagation of a Pearcey beam in uniaxial crystals[J]. Chinese Physics B, 2019, 28(2): 024201. doi: 10.1088/1674-1056/28/2/024201 [13] ZHOU G Q, CHEN R P, CHU X X. Propagation of cosh-Airy beams in uniaxial crystals orthogonal to the optical axis[J]. Optics &Laser Technology, 2019, 116: 72-82. [14] XU CH J, WU J H, WU Y, et al. Propagation of the Pearcey Gaussian beams in a medium with a parabolic refractive index[J]. Optics Communications, 2020, 464: 125478. doi: 10.1016/j.optcom.2020.125478 [15] LIAN M, GU B, ZHANG Y D, et al. Polarization rotation of hybridly polarized beams in a uniaxial crystal orthogonal to the optical axis: theory and experiment[J]. Journal of the Optical Society of America A, 2017, 34(1): 1-6. doi: 10.1364/JOSAA.34.000001 [16] SZTUL H I, ALFANO R R. The Poynting vector and angular momentum of Airy beams[J]. Optics Express, 2008, 16(13): 9411-9416. doi: 10.1364/OE.16.009411 [17] ALLEN L, PADGETT M J. The Poynting vector in Laguerre-Gaussian beams and the interpretation of their angular momentum density[J]. Optics Communications, 2000, 184(1-4): 67-71. doi: 10.1016/S0030-4018(00)00960-3 [18] CHENG K, ZHOU Y, LU G, et al. Vectorial structures of linear-polarized Butterfly-Gauss vortex beams in the far zone[J]. Optics Communications, 2018, 415: 107-114. doi: 10.1016/j.optcom.2018.01.025 -
下载:
点击查看大图
计量
- 文章访问数: 293
- HTML全文浏览量: 242
- PDF下载量: 294
- 被引次数: 0
